23.4 Test de Engle-Granger

Datos diarios de precios de crudo:

• WTI: West Texas Intermediate es una corriente de crudo producido en Texas y el sur de Oklahoma y es utilizado como punto de referencia en la fijación de precios del petróleo.
• Brent -Tipo de petróleo que se extrae principalmente del mar del Norte. Marca la referencia en los mercados europeos.

Ambas series exhiben una tendencia creciente y no parecen alejarse entre ellas. También parece razonable asumir que siguen una relación de equilibrio de largo plazo a la que intentan volver.

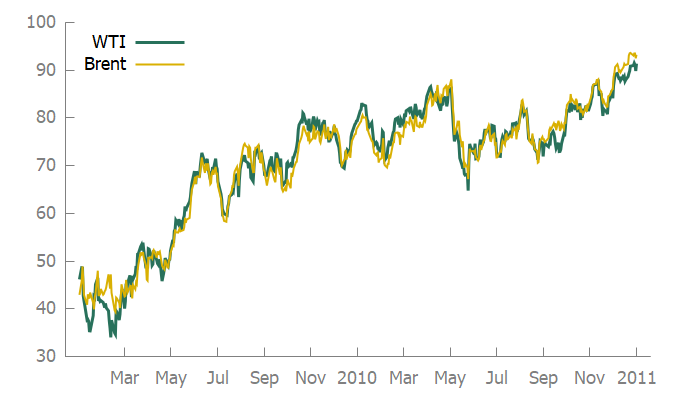
El Test de Engle-Granger ayuda a descubrir si dos series están cointegradas.

• Paso 1: Determinar $d$ - de $I(d)$ - para la primera serie

• Paso 2: Determinar $d$ - de $I(d)$ - para la primera serie

• Paso 3: Estimar la regresión de cointegración: $$Y_t=\beta_1+\beta_2X_t+\epsilon_t$$

• Paso 4: Determinar $d$ - de $I(d)$ - para $\epsilon_t$

  • $H_0:$ Unit root (i.e, $(Y_t)$ y $(X_t)$ no están cointegradas)
  • $H_1:$ No Unit root (i.e, $(Y_t)$ y $(X_t)$ están cointegradas)

Paso 1: ADF para $(Y_t)$

Al primer paso consiste en realizar el test de Dickey-Fuller para la siguiente prueba de hipótesis:

• $H_0:$ La serie $(Y_t),$ en nivel, contiene una raíz unitaria.
• $H_1:$ La serie $(Y_t),$ en nivel, no contiene una raíz unitaria.

Como p-value > 0.05 no existe evidencia empírica para rechazar la hipótesis nula, por lo tanto se puede concluir que la serie $(Y_t),$ en nivel, contiene una raíz unitaria.

Con base en el test anterior decimos que $d =1$ para $(Y_t).$ Es decir, la serie necesita ser diferenciada para ser estacionaria.

Paso 2: ADF para $(X_t)$

El segundi paso consiste en realizar el test de Dickey-Fuller para la siguiente prueba de hipótesis:

• $H_0:$ La serie $(X_t),$ en nivel, contiene una raíz unitaria.
• $H_1:$ La serie $(X_t),$ en nivel, no contiene una raíz unitaria.

Como p-value > 0.05 no existe evidencia empírica para rechazar la hipótesis nula, por lo tanto se puede concluir que la serie $(X_t),$ en nivel, contiene una raíz unitaria.

Con base en el test anterior decimos que $d =1$ para $(X_t).$ Es decir, la serie necesita ser diferenciada para ser estacionaria.

Paso 3: Estimar $(Y_t) = \beta_0 + \beta_1 (X_t) + \epsilon_t$

Los pasos 3 y 4 se pueden realizar directamente en Gretl.

El paso 3 consiste en ajustar la regresión de cointegración y guardar los resíduos.

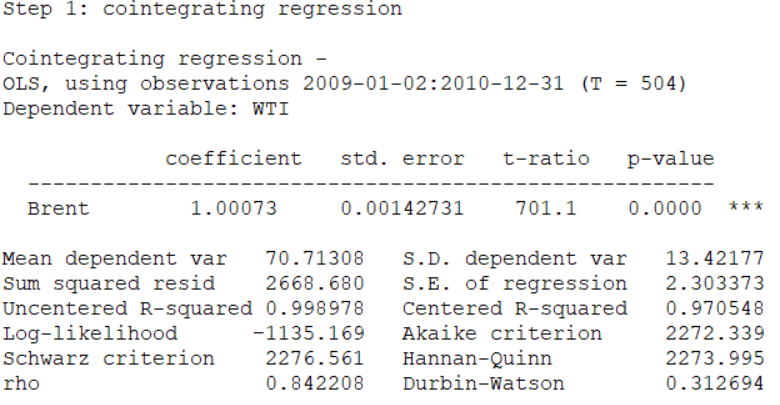
Paso 4: ADF para $\epsilon_t$

El último paso consiste en testar:

• $H_0:$ La serie $(\epsilon_t),$ en nivel, contiene una raíz unitaria.
• $H_1:$ La serie $(\epsilon_t),$ en nivel, no contiene una raíz unitaria.

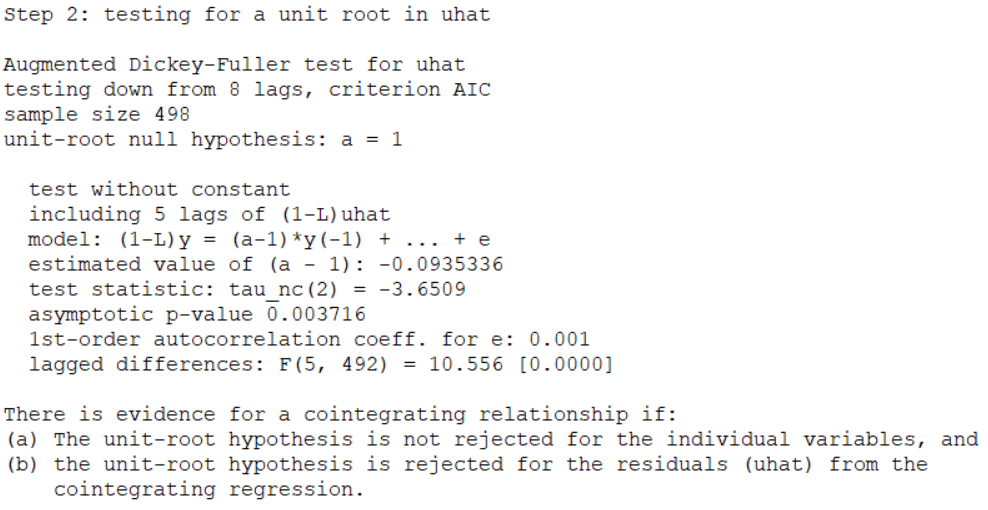
Como p-value < 0.05 existe evidencia empírica para rechazar la hipótesis nula, por lo tanto se puede concluir que la serie $(\epsilon_t),$ en nivel, no contiene una raíz unitaria.

Con base en el test anterior decimos que la serie $(\epsilon_t)$ es estacionaria y, por lo tanto, $(Y_t)$ y $(X_t)$ están cointegradas.