18.2 Estacionariedad
Se dice que un *proceso estocástico es estacionario en sentido estricto si todas las variables aleatorias que componen el proceso están idénticamente distribuidas, independientemente del momento del tiempo en que se estudie el proceso.
Es decir, la función de distribución de probabilidad de cualquier conjunto de \(k\) variables (siendo \(k\) un número finito) del proceso debe mantenerse estable (inalterable) al desplazar las variables \(s\) períodos de tiempo tal que, si \(P(Y_{t+1}, Y_{t+2}, …, Y_{t+k} )\) es la función de distribución acumulada de probabilidad, entonces:
\[ P(Y_{t+1},Y_{t+2},…,Y_{t+k}) = P(Y_{t+1+s}, Y_{t+2+s},…,Y_{t+k+s}),\ \ \forall t, k, s \]
Sin embargo, la versión estricta de la estacionariedad de un proceso suele ser excesivamente restrictiva. Por ello generalmente se utiliza la estacionariedad en sentido débil o de segundo orden, la cual se da cuando la media del proceso es constante e independiente del tiempo, la varianza es finita y constante, y el valor de la covarianza entre dos periodos depende únicamente de la distancia o desfase entre ellos, sin importar el momento del tiempo en el cual se calculan.
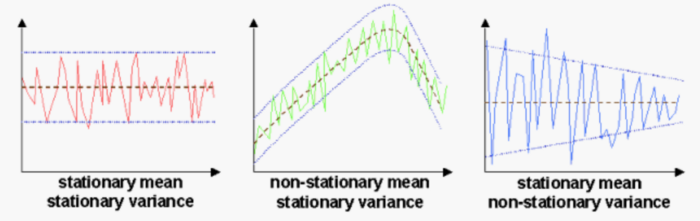
Una serie temporal es estacionaria (en sentido débil) cuando el nivel y las covarianzas de la serie no se alteran con el transcurso del tiempo.
En otras palabras, una serie temporal es estacionaria cuando se desarrolla en el tiempo aleatoriamente alrededor de una media constante, mostrando alguna forma de equilibrio estable.
De forma simple, una serie temporal es estacionaria si su comportamiento no cambia con el tiempo. Esto significa, por ejemplo, que los valores siempre tienden a variar en torno al mismo nivel y que su variabilidad es constante a lo largo del tiempo. Para las series estacionarias se dispone de mucha teoría ya que su comportamiento es bien conocido. Por ello, juegan un papel fundamental papel fundamental en el estudio de las series temporales.
¿Por qué resulta importante para el investigador que el proceso analizado sea estacionario?
La razón fundamental es que los modelos de predicción de series temporales que veremos a continuación están diseñados para ser utilizados con procesos de este tipo. Si las características del proceso cambian a lo largo del tiempo, resultará difícil representar la serie para intervalos de tiempo pasados y futuros mediante un modelo lineal sencillo, no pudiéndose por tanto realizar previsiones fiables para la variable en estudio.
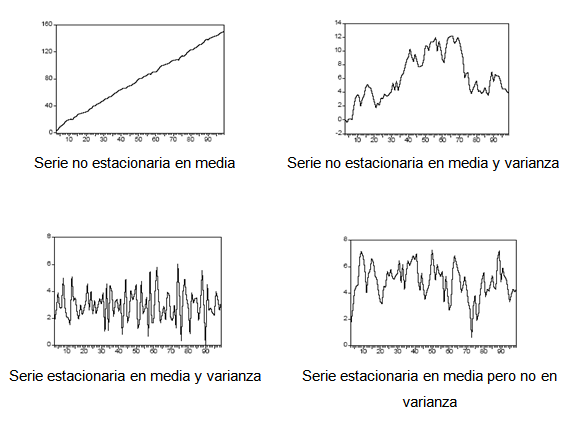
Sin embargo, por regla general, las series económicas no son series que procedan de procesos estacionarios, sino que suelen tener una tendencia, ya sea creciente o decreciente, y variabilidad no constante. Dicha limitación en la práctica no es tan importante porque las series no estacionarias se pueden transformar en otras aproximadamente estacionarias después de aplicar diferencias a la serie en una ó más etapas.