23.2 Test de Dickey-Fuller

Considerando el proceso estocástico:

$$Y_t = \phi Y_{t-1} + \omega_t$$

donde $\mid \phi \mid \leq 1$ y $\omega_t$ es ruido blanco (white noise).

Si $\mid \phi \mid = 1,$ tenemos una raíz unitaria. En particular, si $\phi = 1,$ tenemmos un camino aleatorio (random walk sin constante), que es un proceso no estacionario. No consideramos el caso $\mid \phi \mid > 1,$ ya que en este caso el proceso se llama explosivo y aumenta con el tiempo.

El test de Dickey-Fuller es una alternativa para determinar si el proceso anterior tiene una raíz unitaria. El procedimiento utilizado es bastante sencillo.

Primero se clacula la primera diferencia, i.e.,

$$\begin{aligned} Y_t - Y_{t-1} & =\phi Y_{t-1} + \omega_t - Y_{t-1} \\ Y_t - Y_{t-1} & =(\phi -1)Y_{t-1} + \omega_t \\ \end{aligned}$$ Si usamos el operador diferencia $\nabla Y_t = Y_t - Y_{t-1}$ y hacemos $\beta = (\phi -1),$ la ecuación anterior es

$$\nabla Y_t= \beta Y_{t-1} + \omega_t$$ donde $\beta \leq 0$ y de aquí, el test para $\pi$ se transforma en un test para la pendiente (slope) de una regresión lineal: $H_0: \beta=0.$ Como $\beta$ no puede ser positivo, se realiza una prueba de hipótesis de una cola:

• $H_0:$ $\beta=0$ (equivalente a $\phi=1$)
• $H_1:$ $\beta<0$ (equivalente a $\phi<1$)

Si $\hat{\beta}$ es el estimador de mínimos cuadrados ordinarios de $\beta,$ y, por lo anto $\hat{\phi} = 1+ \hat{\beta},$ para $N$ grande se tiene:

$$\sqrt n (\phi-\hat{\phi}) \sim N(0, \sqrt{1-\phi^2})$$ Para concluir sobre la prueba no podemos usar la distribución $t$-Student como en el caso de la regresión lineal. En su lugar se usa la tabla de Dickey-Fuller. Si el valos estimado es menor que el valor crítico, se rechaza $H_0$. En cambio, si el p-valor es grande, no se rechaza $H_0$ y se concluye que existe una raiz unitaria y, por lo tanto, la serie es no estacionaria.

Existen varias versiones del test de Dickey-Fuller:

Versión	Description	Equation
Type 0	Sin constante, sin Tendencia	$\nabla Y_t= \beta_1 Y_{t-1} + \omega_t$
Type 1	Con constante, sin Tendencia	$\nabla Y_t= \beta_0 + \beta_1 Y_{t-1} + \omega_t$
Type 2	Con constante, con Tendencia	$\nabla Y_t= \beta_0 + \beta_1 Y_{t-1} + \beta_2 t + \omega_t$

Cada versión de la prueba utiliza un conjunto diferente de valores críticos en la tabla Dickey-Fuller. Es muy importante seleccionar la versión correcta de la prueba para la serie temporal que se está analizando.

• Serie en nivel:

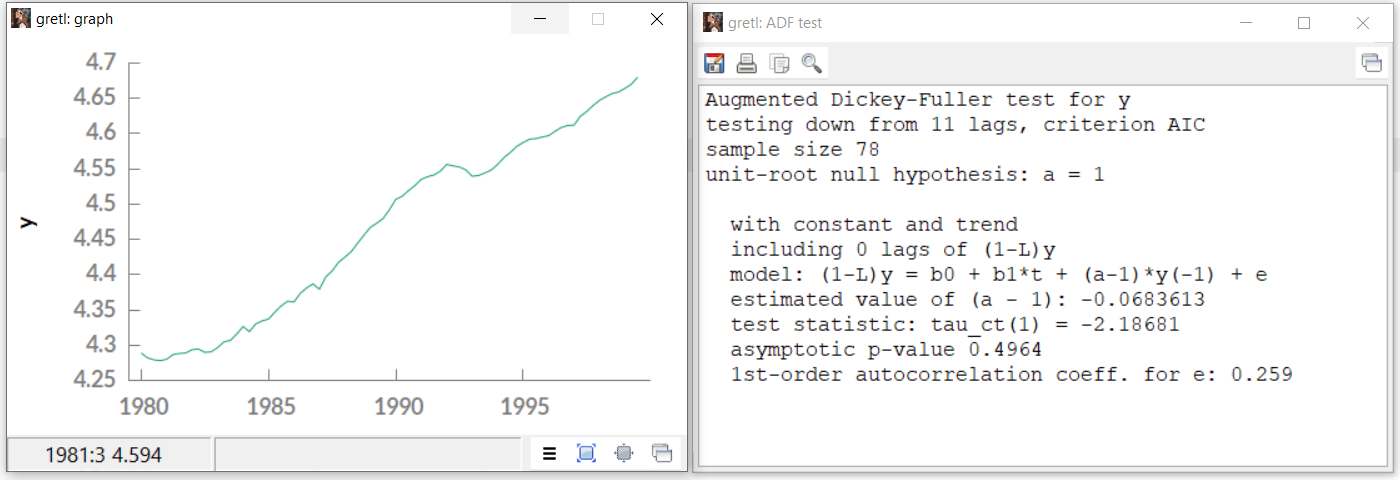
Figure 23.1: ADF: Prueba en una serie en nivel.

• Serie diferenciada:

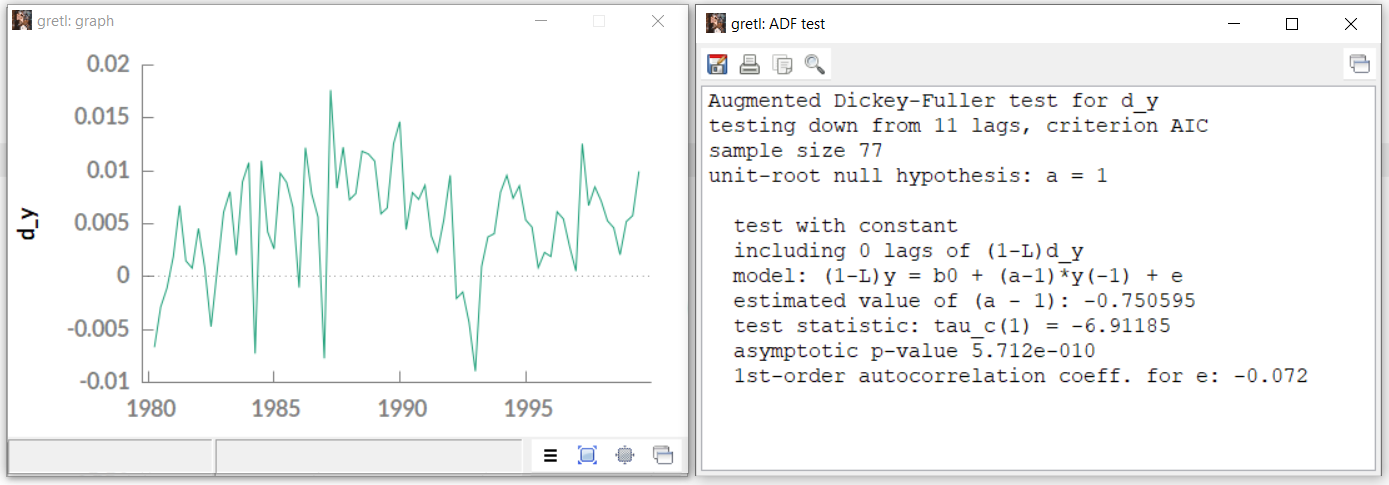
Figure 23.2: ADF: Prueba en una serie en primeras diferencias.

La presencia de una raíz unitaria significa que la serie temporal es no estacionaria. Así mismo, el número de raíces unitarias contenidas en la serie corresponde al número de operaciones de diferenciación necesarias para que la serie sea estacionaria.

23.2.1 Test de Dickey-Fuller Aumentado

La prueba de Dickey-Fuller aumentada (ADF) se ha desarrollado sobre la base de la prueba presentada en la sección anterior. Se trata de una de las formas más comunes de prueba de raíz unitaria.

La prueba ADF amplía la ecuación de la prueba Dickey-Fuller para incluir procesos autoregresivos de alto orden en el modelo.

$$\nabla Y_t= \beta_0 + \beta_1 Y_{t-1} + \beta_2 t + \psi_1 \nabla Y_{t-1} + \psi_2 \nabla Y_{t-2} + \ldots + + \psi_p \nabla Y_{t-p} + \omega_t$$

Sólo se añaden términos de diferenciación. El resto de la ecuación sigue siendo la misma. Esto añade más rigor a la prueba. La hipótesis nula es la misma que la de la prueba Dickey Fuller.

La intuición detrás de la prueba es que si la serie se caracteriza por un proceso de raíz unitaria, entonces el nivel rezagado de la serie ($Y_{t-1}$) no proporcionará ninguna información relevante para predecir el cambio en $Y_{t}$ además de la obtenida en los cambios rezagados ($\nabla y_{t-k}$). En este caso $\beta =0$ y no se rechaza la hipótesis nula. Por el contrario, cuando el proceso no tiene raíz unitaria, es estacionario y, por tanto, presenta reversión a la media, por lo que el nivel retardado proporcionará información relevante para predecir el cambio de la serie y se rechazará la nula de una raíz unitaria.

Un punto clave que hay que recordar aquí es: Dado que la hipótesis nula supone la presencia de una raíz unitaria, es decir,$H_0:$ $\beta=0$ (equivalente a $\phi=1$), el valor $p$ obtenido debe ser inferior al nivel de significación (digamos 0.05) para rechazar la hipótesis nula. De este modo, se infiere que la serie es estacionaria (y no al contrario!).