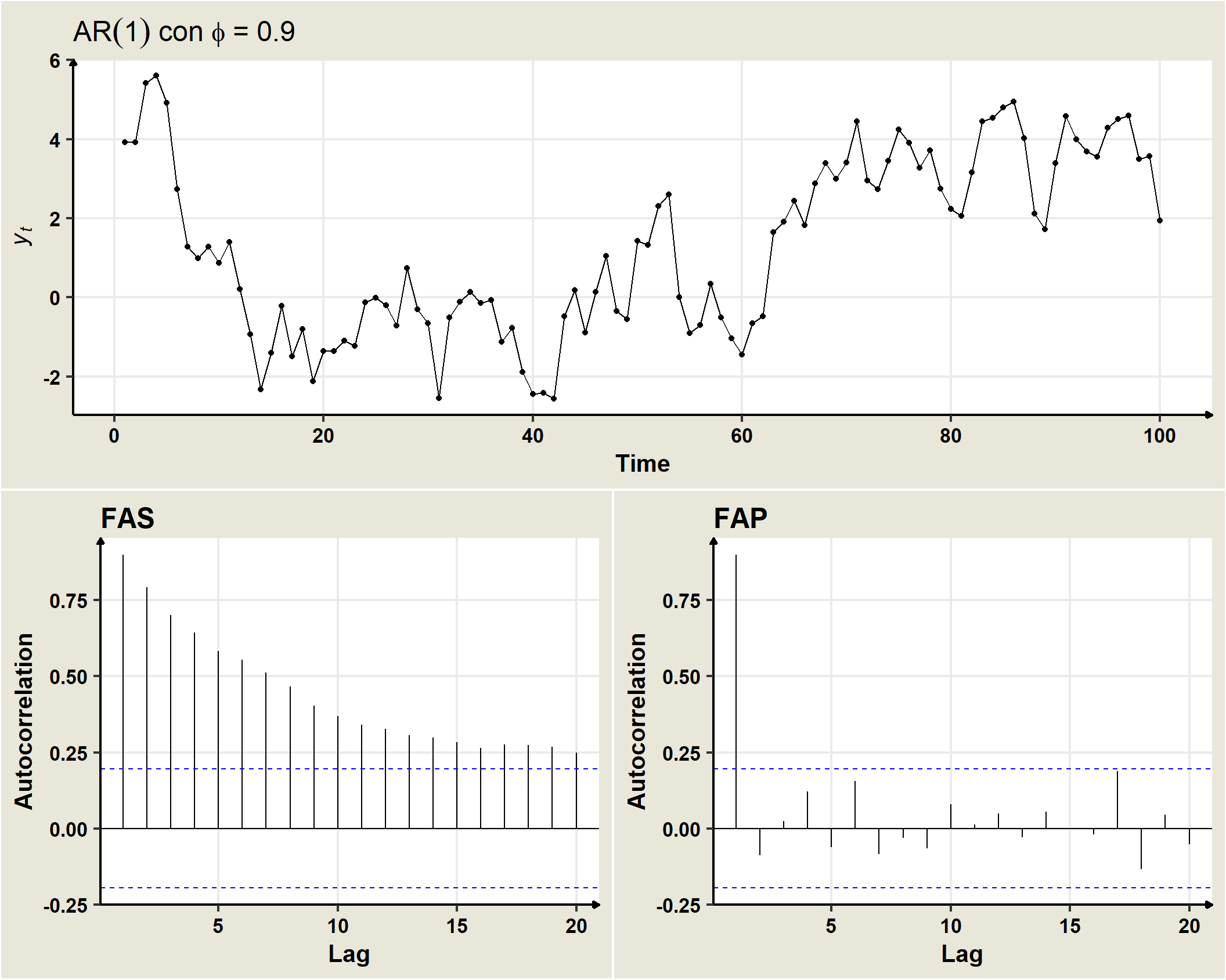
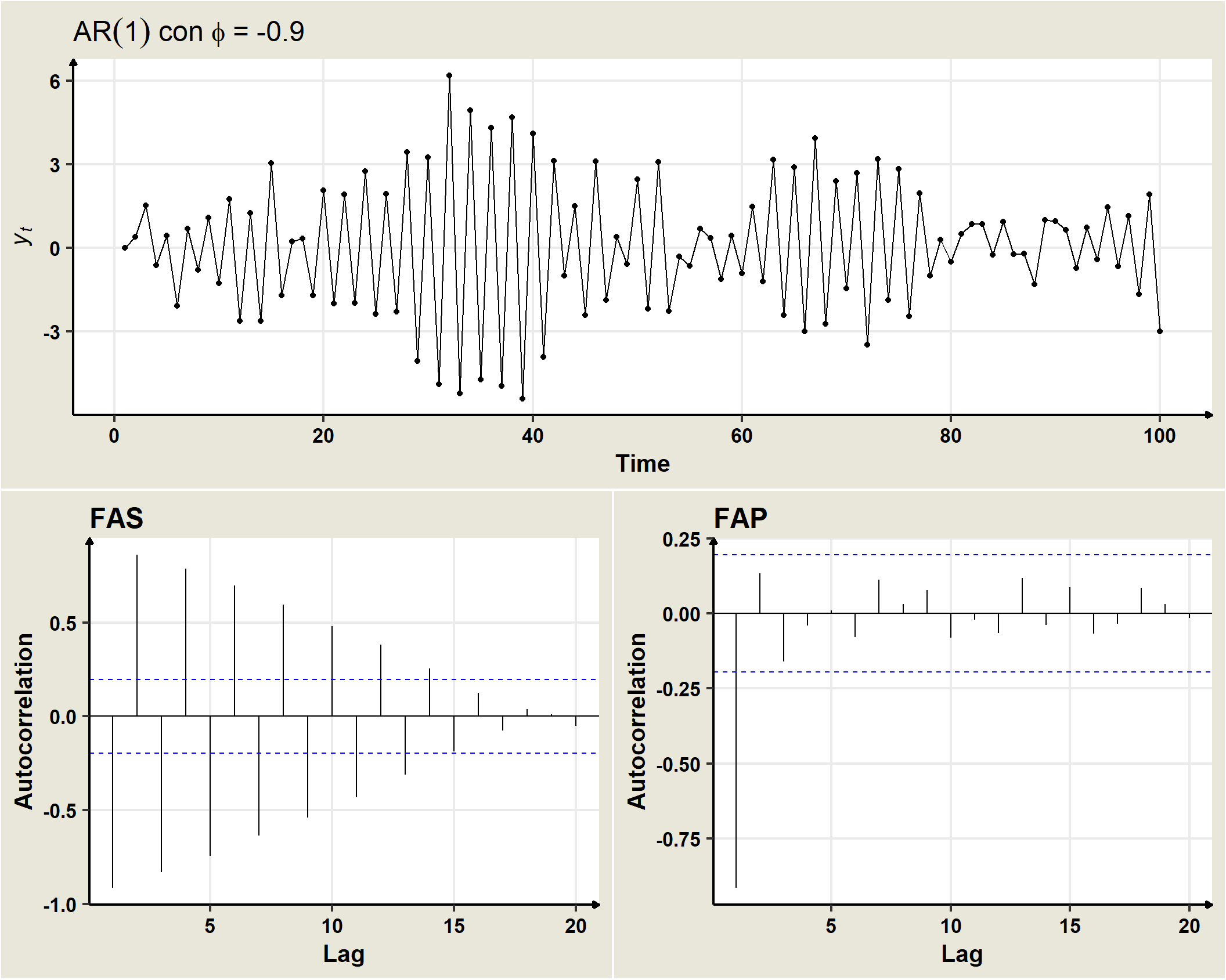
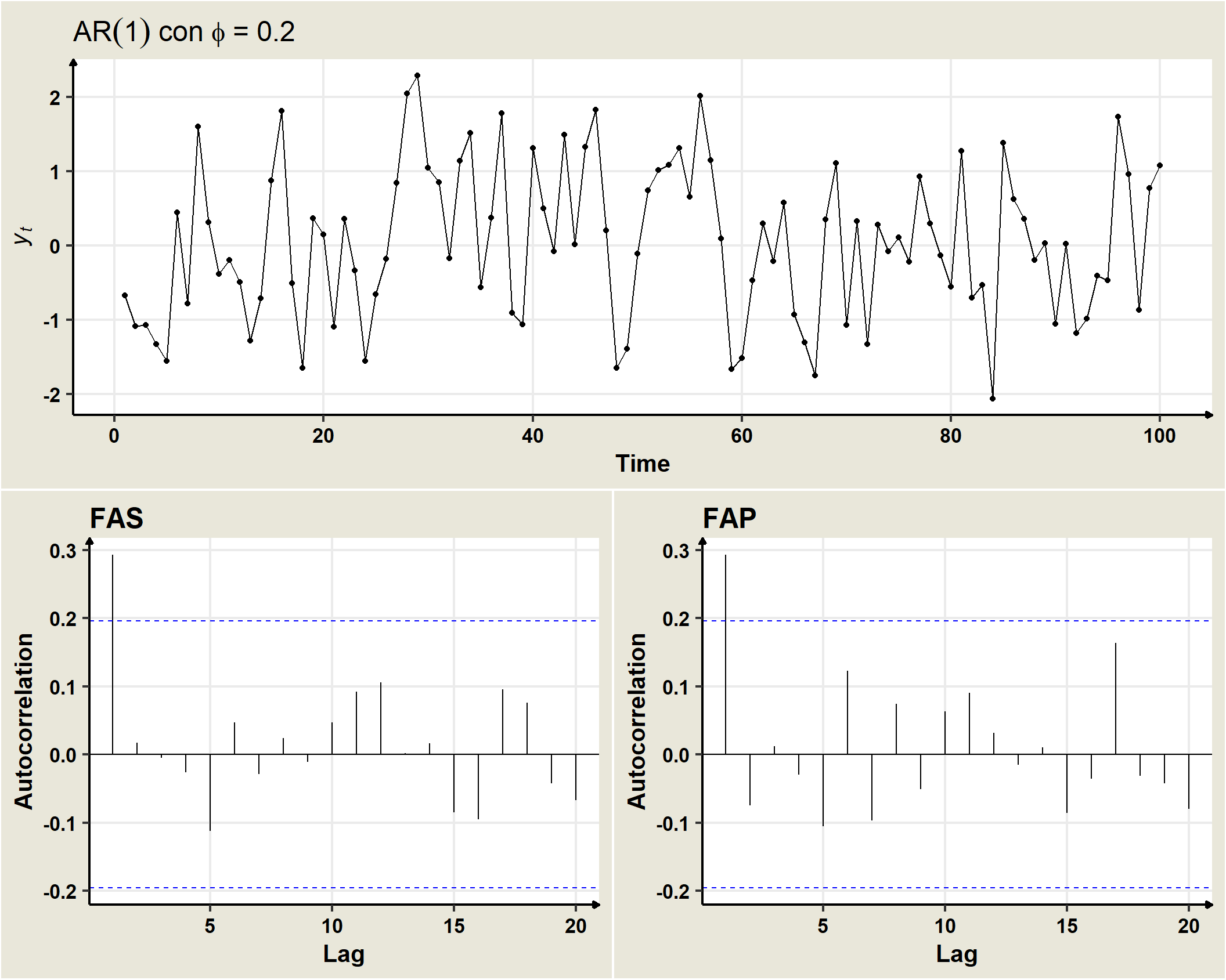
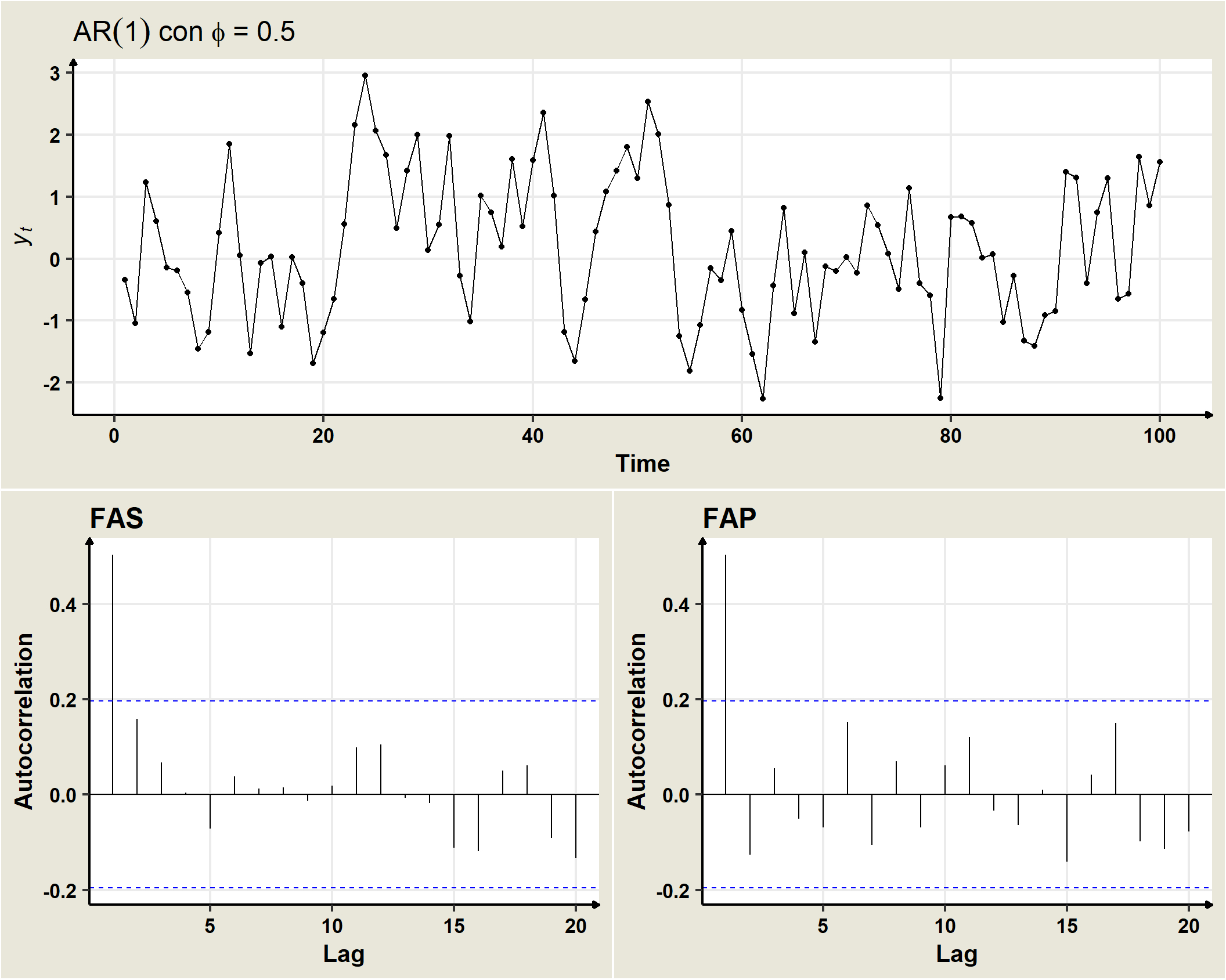
19.4 AR(1)
Un proceso estocástico estacionario \((Y_t)\) sigue un modelo AR(1) si
\[Y_t=\delta +\phi_1 Y_{t-1}+\omega_t, \quad \forall t=\pm1, \pm2, \pm3, \ldots\]
donde \((w_t)\) es un ruido blanco con media cero y varianza \(\sigma^2_\omega, \,\, \rightarrow \,\, \omega_t \sim N(0,\sigma^2_\omega).\)
Si el proceso es estacionario en media y varianza entonces se cumple que \(E(Y_t) = E(Y_{t-1})\) y \(Var (Y_t) = Var(Y_{t-1}), \forall t\) de forma que:
\[ E(Y_t) = E(Y_{t-1})=\mu=\delta +\phi_1\mu \rightarrow \mu=\frac{\delta}{1-\phi_1} \] \[ \gamma_0 = Var(Y_t) = Var(Y_{t-1})= \phi_1^2\gamma_0 +\sigma_\omega^2 \rightarrow \gamma_0 = \frac{\sigma_\omega^2}{1-\phi_1^2} \]
La condición a cumplir para que \(\mu\) y \(\gamma_0\) sean positivas y finitas es que \(|\phi_1|<1\) (condición de invertibilidad). En ese caso, el proceso será estacionario en media y varianza. Del mismo modo, si el proceso es estacionario, también se verificará para las covarianzas que:
\[ \begin{aligned} \gamma_k & = E[Y_t Y_{t-k}] - E[Y_t]E[Y_{t-k}]\\ & = E[(\phi_1Y_{t-1} + \omega_t) Y_{t-k}]\\ & = \phi_1E[Y_{t-1}Y_{t-k}] + E[\omega_t Y_{t-k}]\\ & = \phi_1 \gamma_{k-1} =\phi_1^2 \gamma_{k-2} = \phi_1^3 \gamma_{k-3} =\ldots = \phi_1^k \gamma_{0}\\ & \rightarrow \rho_k = \dfrac{\gamma_k}{\gamma_0}=\dfrac{\phi_1^k\gamma_0}{\gamma_0}=\phi_1^k \end{aligned} \]
donde, sin pérdida de generalidad se ha supuesto \(E[Y_t]=\mu=0\)