19.2 Paseo Aleatorio (Random walk)

Un proceso estocástico no estacionario $(Y_t)$ es un paseo aleatorio o camino al azar cuando:

$$Y_t=Y_{t-1} + \omega_t$$

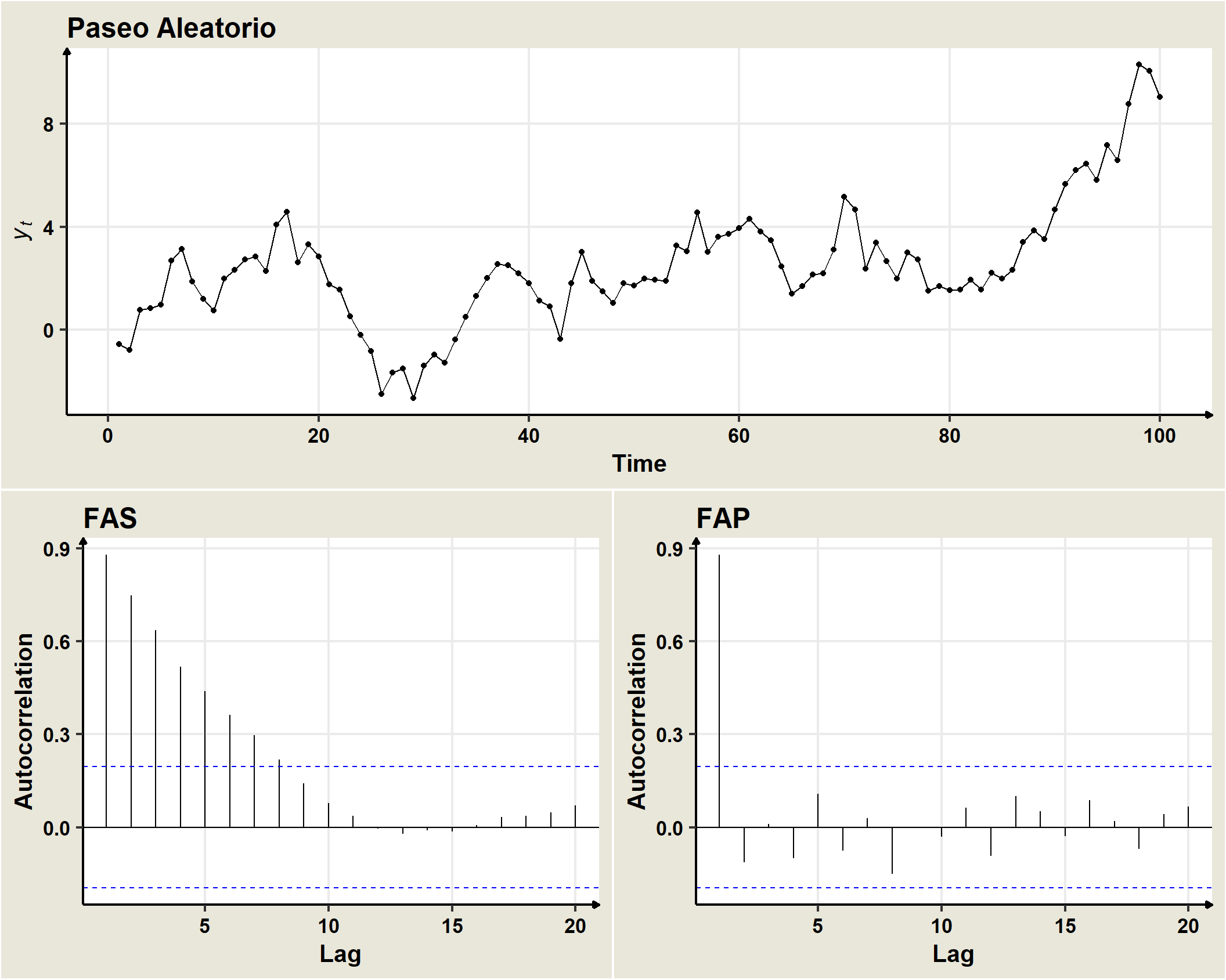
• Un paseo aleatorio es un proceso estocástico cuya primera diferencia es un ruido blanco, esto es

$$Y_t - Y_{t-1}=\omega_t$$ * Algunas veces se incluye un parámetro adicional:

$$Y_t = \mu + Y_{t-1} + \omega_t$$

• Un paseo aleatorio puede escribirse como

$$\nabla Y_t = \mu + \omega_t,$$

de forma que un proceso estocástico no estacionario $(Y_t)$ es un paseo aleatorio cuando su diferencia regular de orden 1 $\left(\nabla Y_{t}\right) \equiv\left(Y_{t}-Y_{t-1}\right)$ es un proceso estacionario.