16.1 Medias Móviles
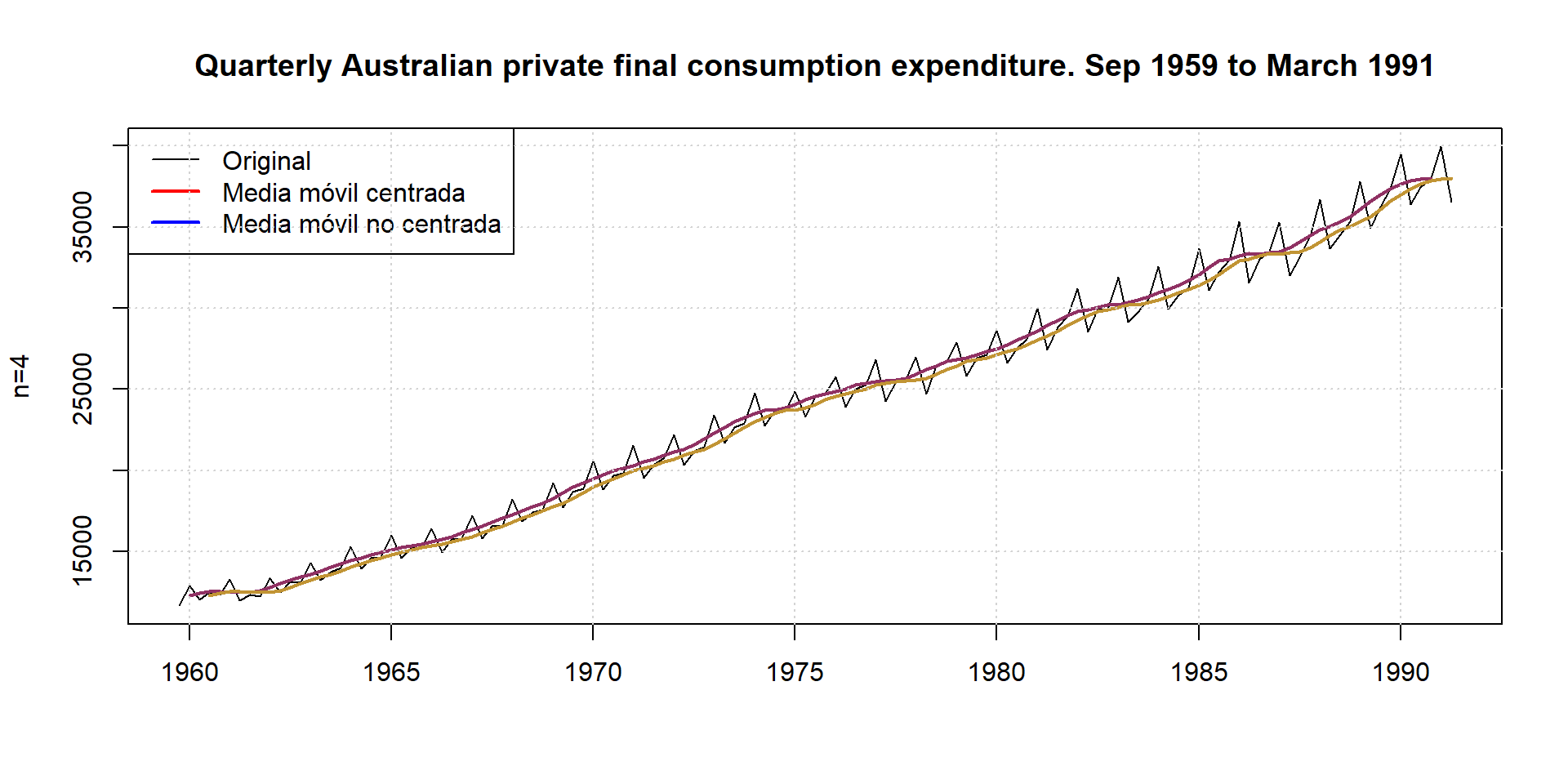
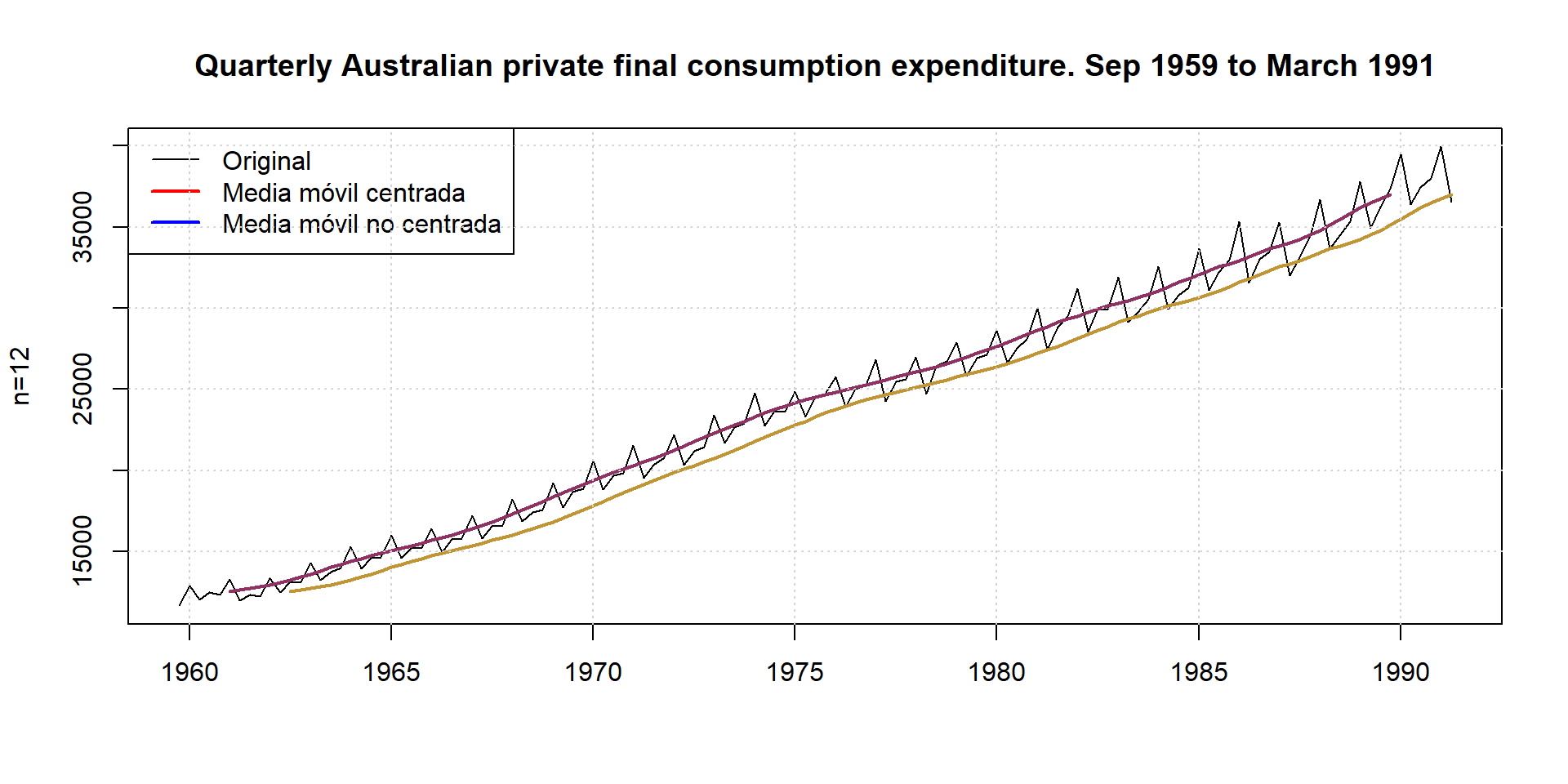
En el análisis de series temporales, el método de medias móviles tiene diversas aplicaciones: este método puede sernos útil si queremos calcular la tendencia de una serie temporal sin tener que ajustarnos a una función previa, ofreciendo así una visión suavizada o alisada de una serie, ya que promediando varios valores se elimina parte de los movimientos irregulares de la serie; también puede servirnos para realizar predicciones cuando la tendencia de la serie tiene una media constante.
Una media móvil es una media aritmética que se caracteriza porque toma un valor para cada momento del tiempo y porque en su cálculo no entran todas las observaciones de la muestra disponible.
Entre los distintos tipos de medias móviles que se pueden construir nos vamos a referir a dos tipos: medias móviles centradas y medias móviles asimétricas. El primer tipo se utiliza para la representación de la tendencia, mientras que el segundo lo aplicaremos para la predicción en modelos con media constante.
Las medias móviles centradas se caracterizan porque el número de observaciones que entran en su cálculo es impar, asignándose cada media móvil a la observación central. Así, una media móvil centrada en \(t\) de longitud \(2n+1\) viene dada por la siguiente expresión:
\[ MM(2n+1)_t=\dfrac{y_{t-n}+y_{t-n+1}+...+y_t+...+y_{t+n-1}+y_{t+n}}{2n+1} \]
Como puede observarse, el subíndice asignado a la media móvil, \(t\), es el mismo que el de la observación central, \(y_t\). Obsérvese también que, por construcción, no se pueden calcular las medias móviles correspondientes a las \(n\) primeras y a las \(n\) últimas observaciones.
Por su parte, en el caso de las medias móviles asimétricas (no centradas) se asigna cada media móvil al período correspondiente a la observación más adelantada de todas las que intervienen en su cálculo. Así, la media móvil asimétrica de \(n\) puntos asociada a la observación \(t\) tendrá la siguiente expresión:
\[ MMA(n)_t=\dfrac{y_{t-n+1}+y_{t-n+2}+...+Y_{t-1}+y_{t}}{n} \]
La utilización de medias móviles implica la elección arbitraria de su longitud u orden, es decir, del número de observaciones que intervienen en el cálculo de cada media móvil. Cuanto mayor sea la longitud, mejor se eliminarán las irregularidades de la serie, ya que al intervenir más observaciones en su cálculo se compensarán las fluctuaciones de este tipo, pero por el contrario, el coste informativo será mayor. Por el contrario, cuando la longitud es pequeña, la media móvil refleja con mayor rapidez los cambios que puedan producirse en la evolución de la serie. Es conveniente, pues, sopesar estos factores al decidir la longitud de la media móvil.