20.1 FAS y FAP teóricas ARMA
El objetivo que se persigue es identificar el proceso que subyace bajo la los datos, lo cual consiste en identificar los órdenes p y q del modelo ARMA que generó la serie temporal.
Las herramientas para identificar a estos procesos son las funciones de autocorrelación simple (FAS) y parcial (FAP).
Los correlogramas permiten la representación de estas funciones que solo tienen sentido dentro del ámbito de los procesos estacionarios porque asumen que la correlación entre dos valores de la serie solo depende de su distancia, no del instante de tiempo al que van referidos.
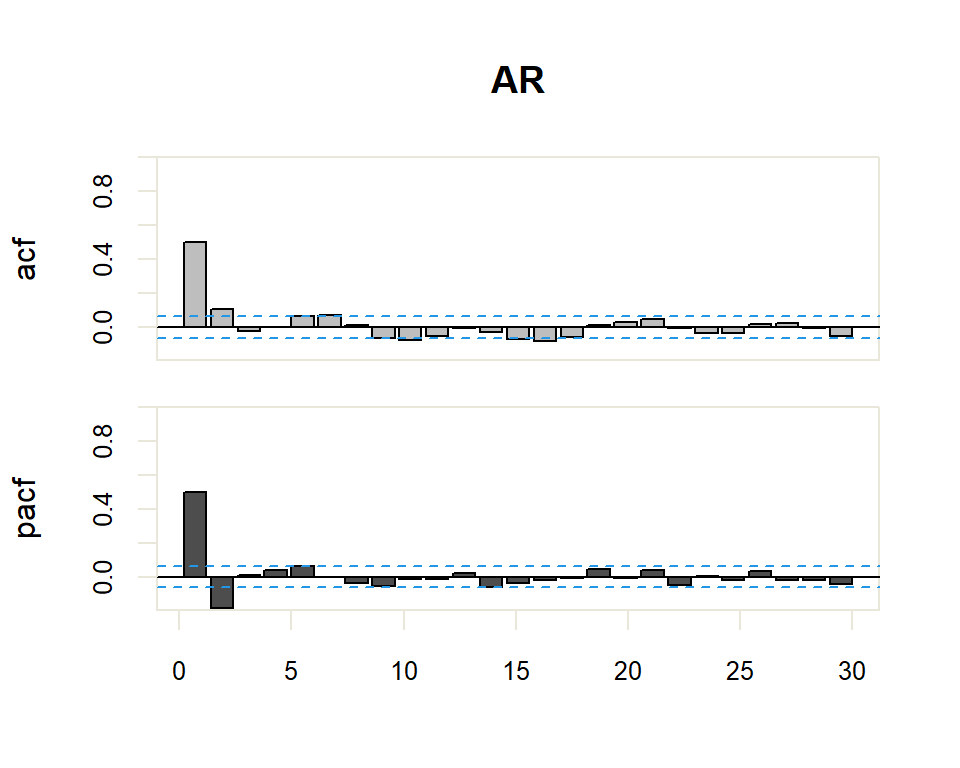
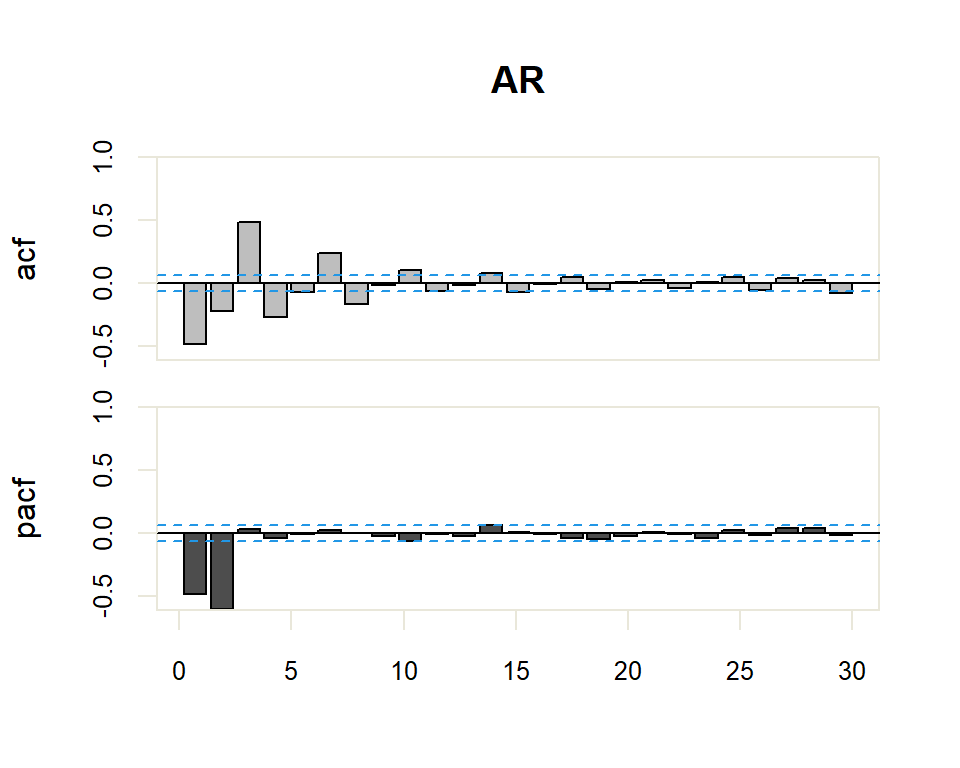
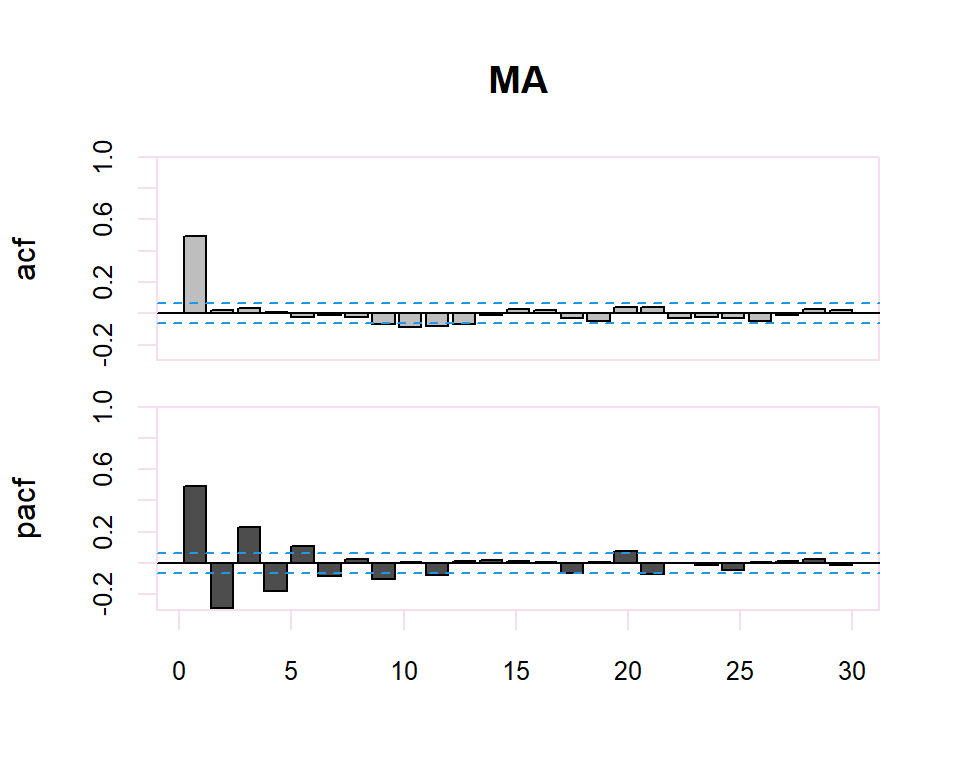
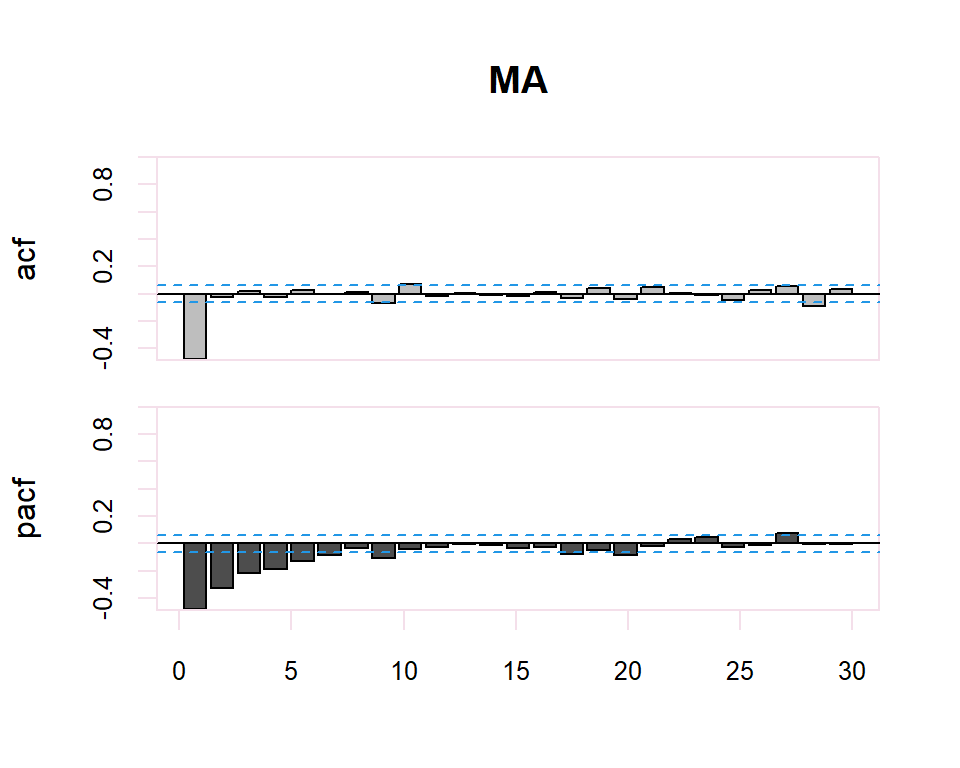
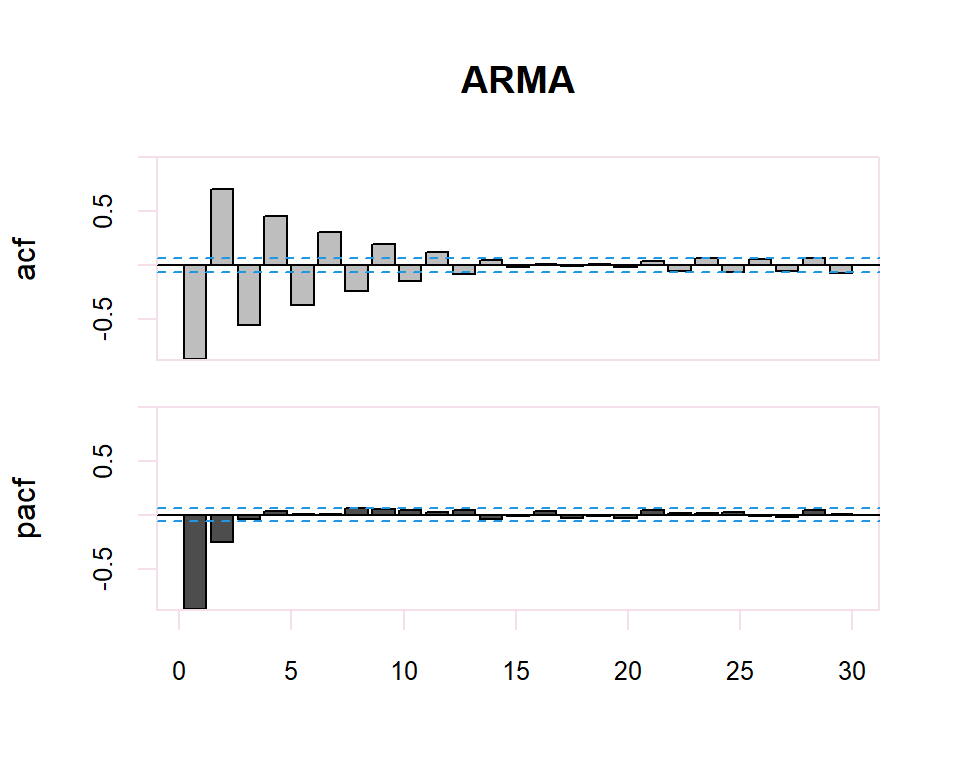
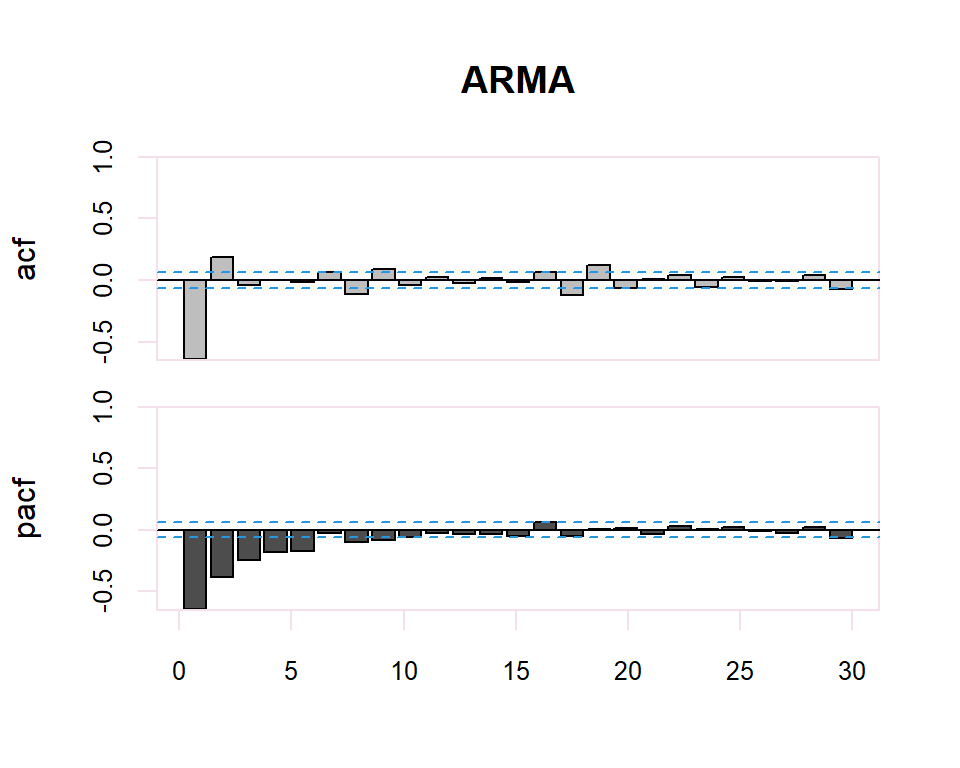
A partir de estos correlogramas, se puede intuir los órdenes p y q del modelo ARMA correspondiente. La dualidad entre los procesos AR y MA se vuelve a poner de manifiesto respecto al patrón que presentan dichos modelos en uno y otro gráfico.
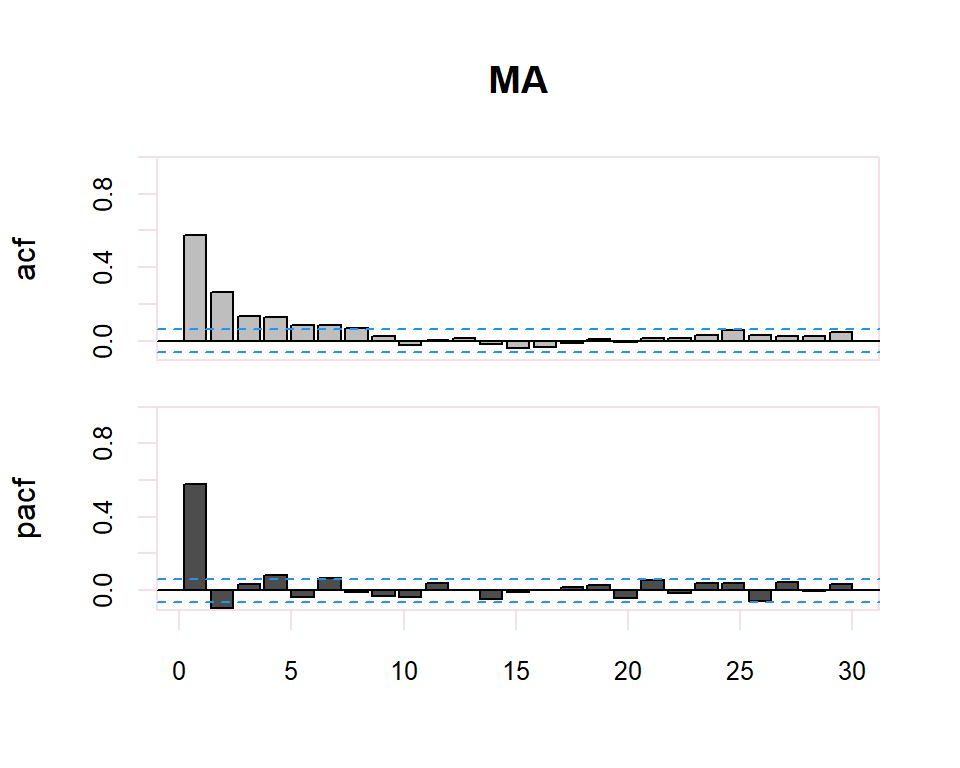
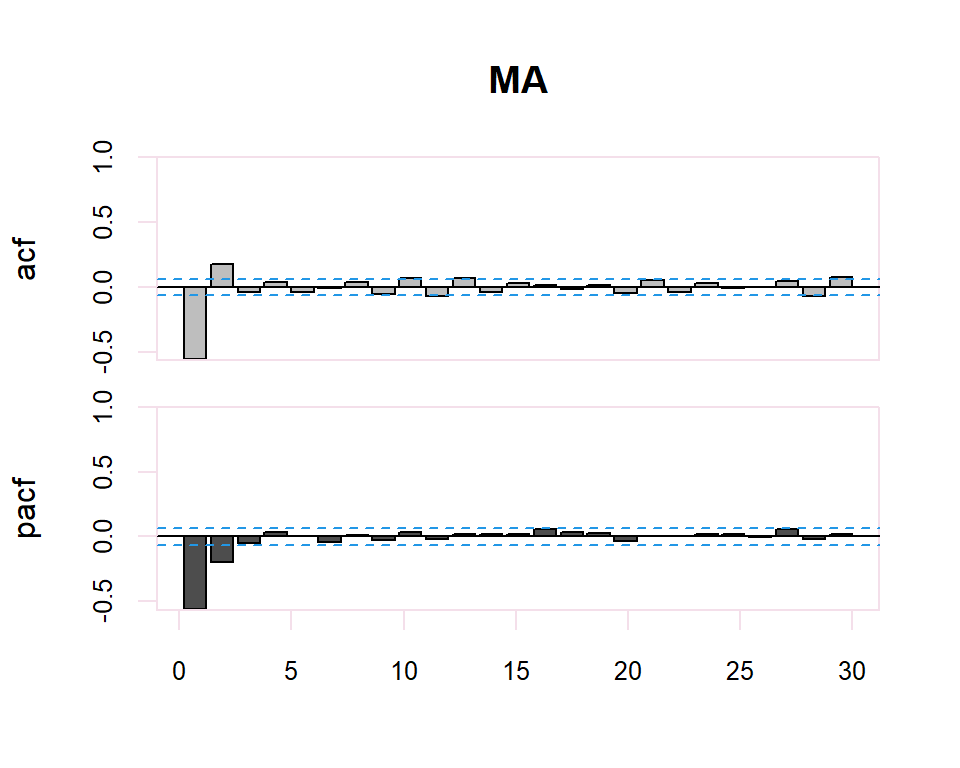
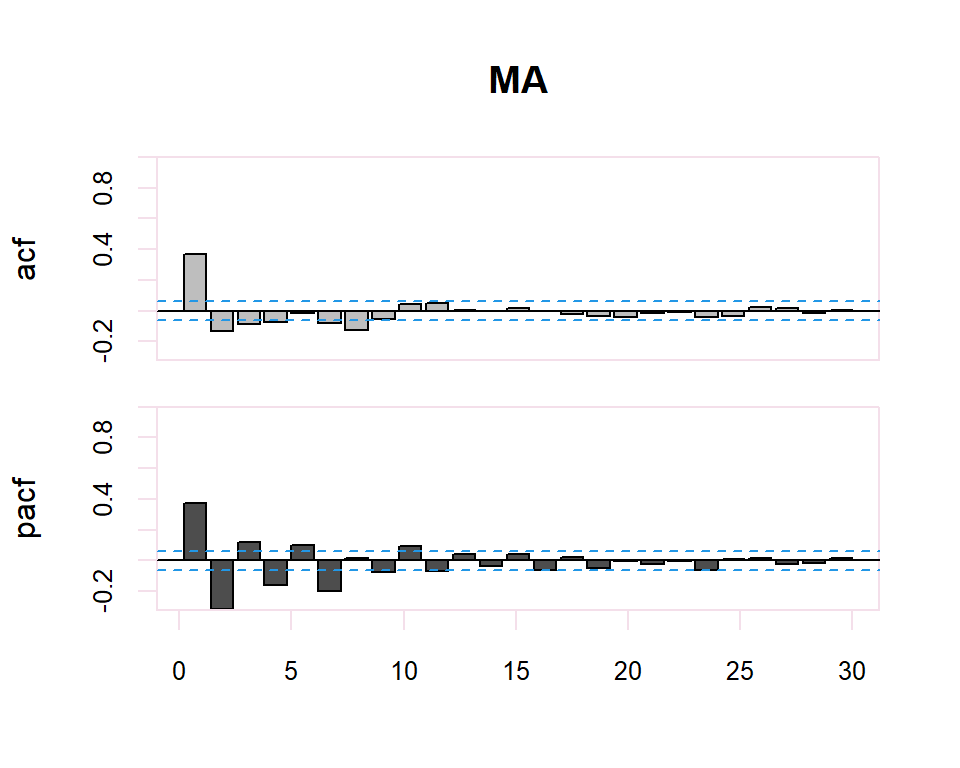
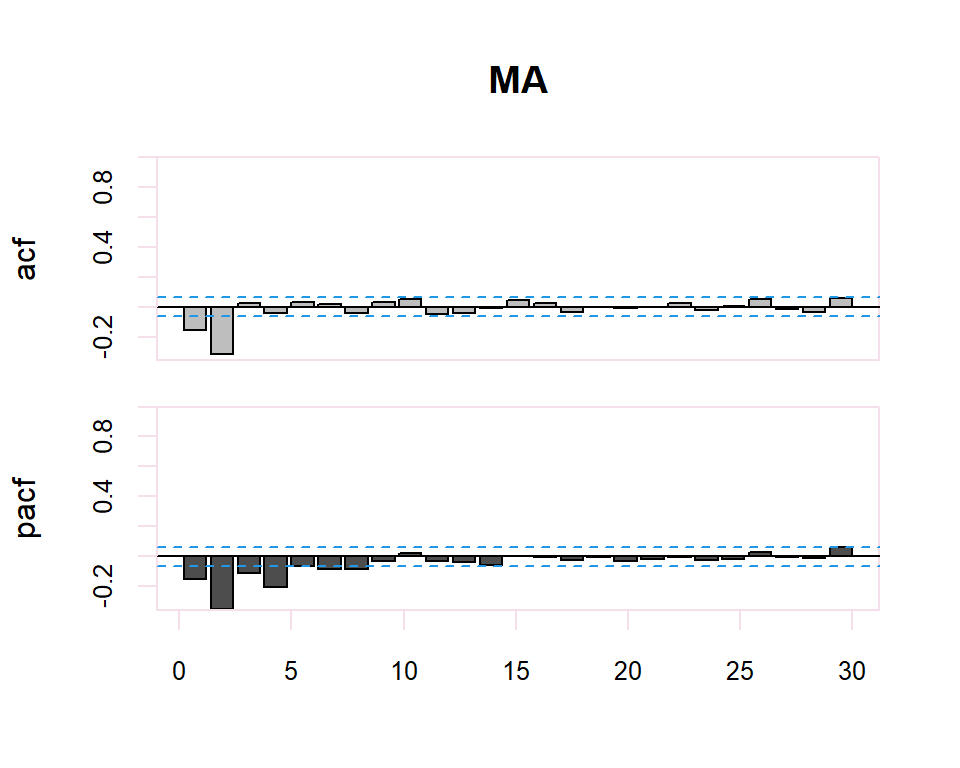
Existe una dualidad entre procesos AR y MA, de manera que la fap de un MA(q) tiene la estructura de la fas de un AR(q), y la FAS de un MA(q) tiene la estructura de la FAP de un AR(q).
20.1.1 AR y MA
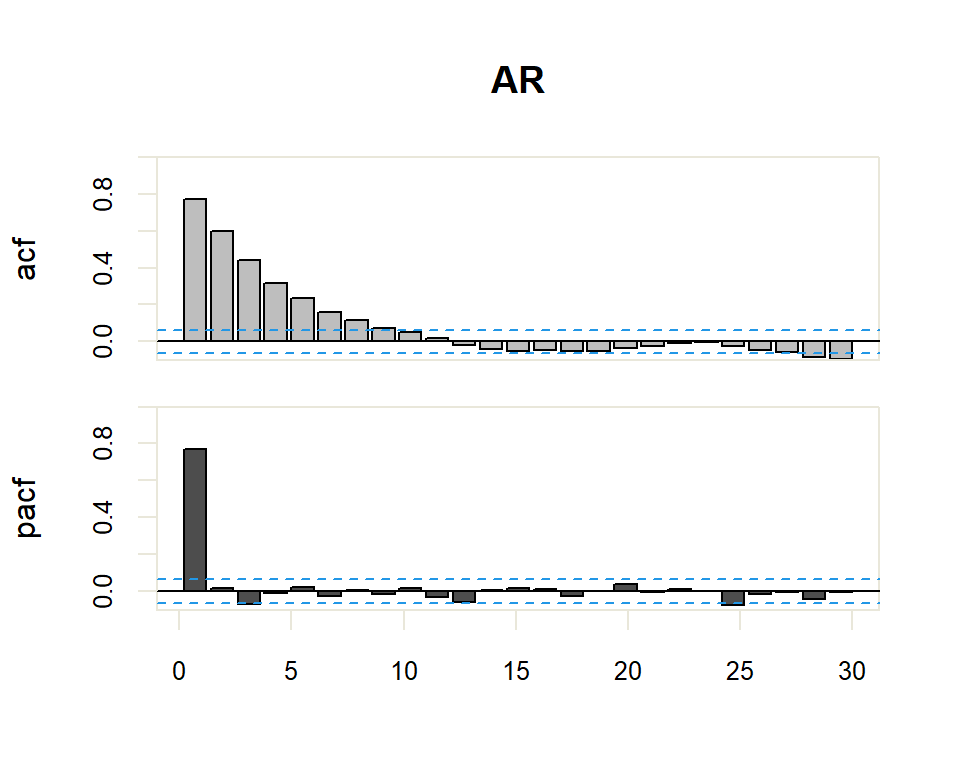
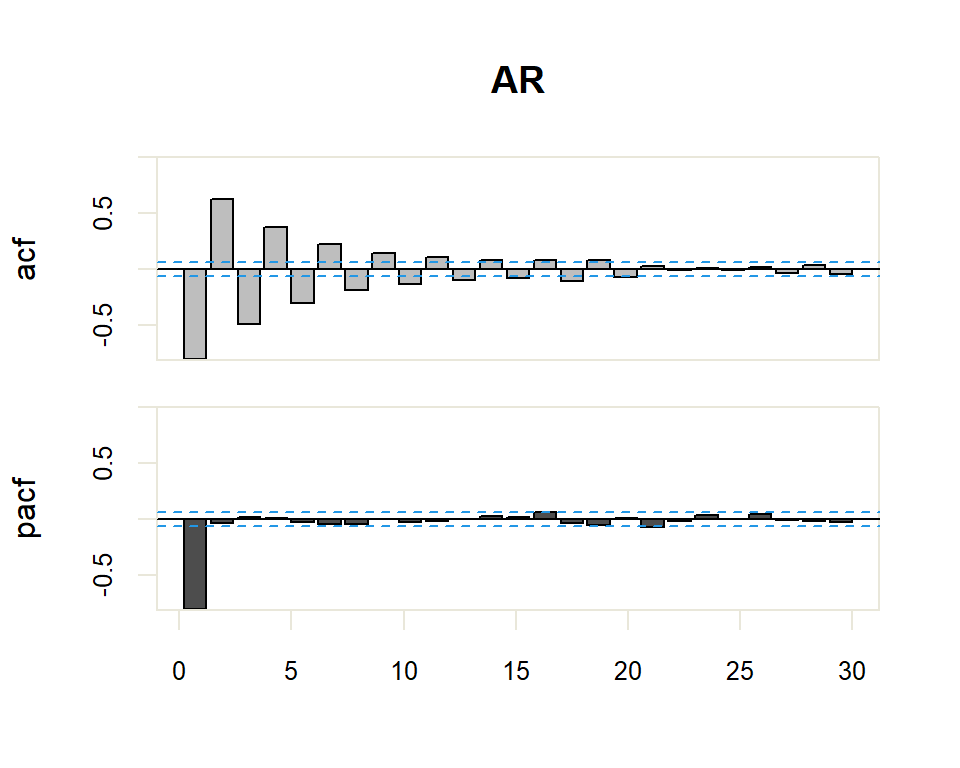
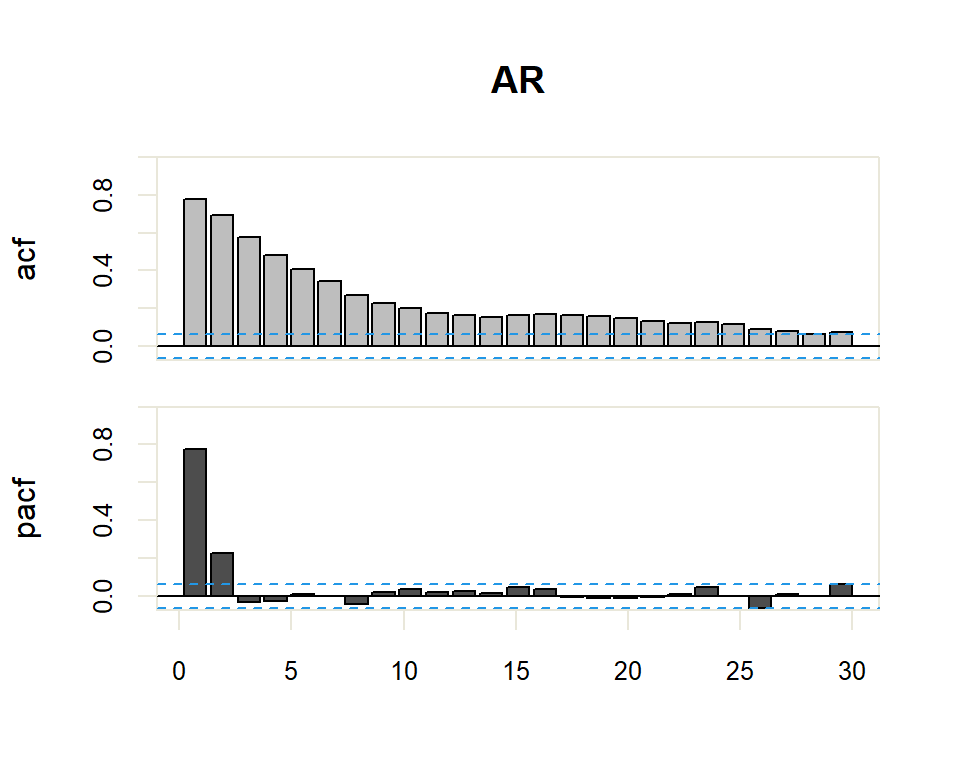
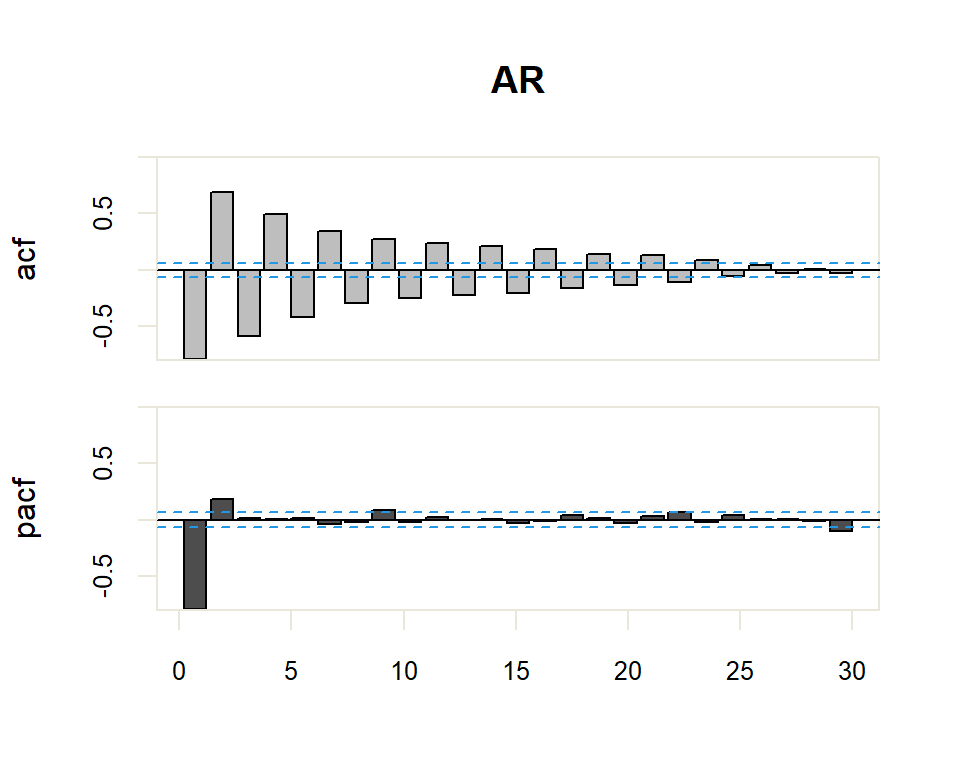
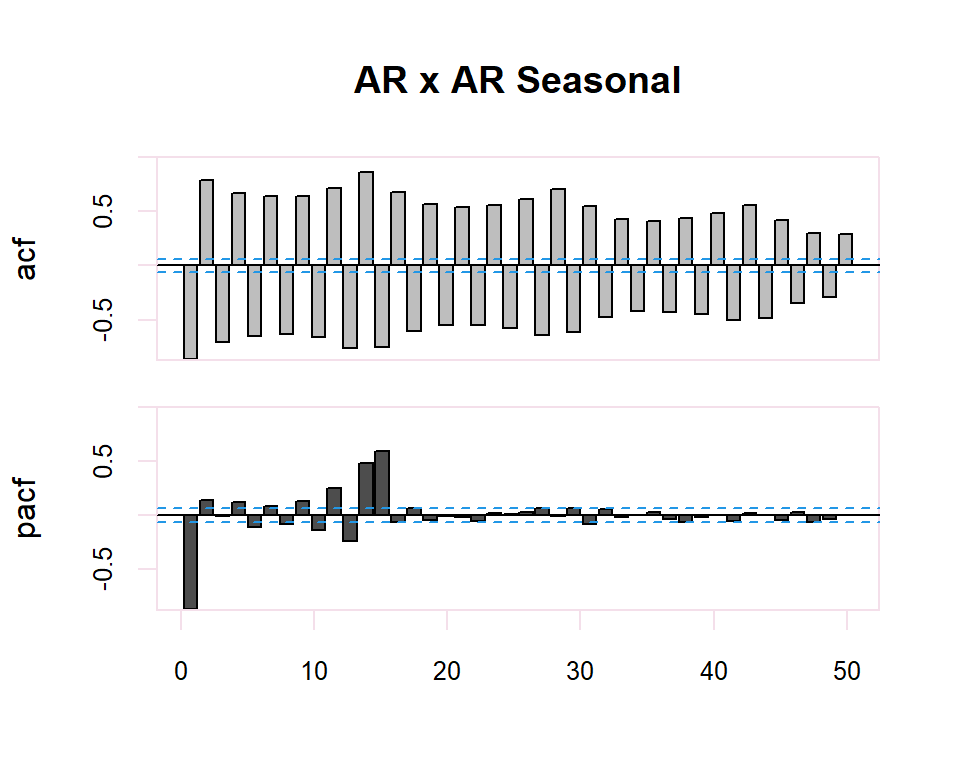
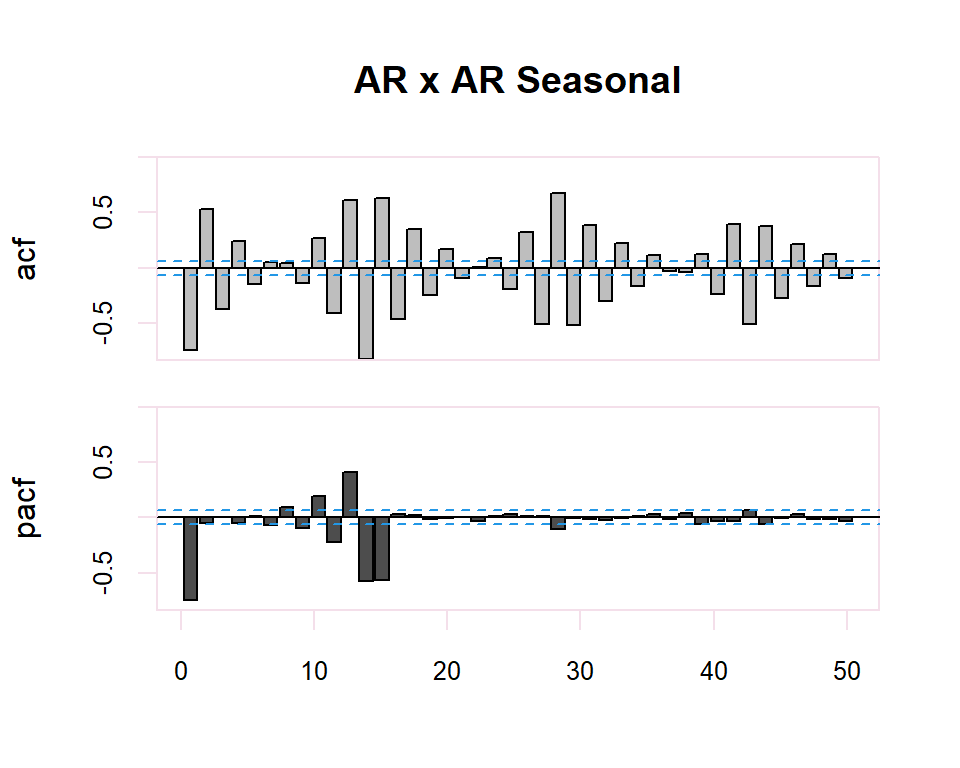
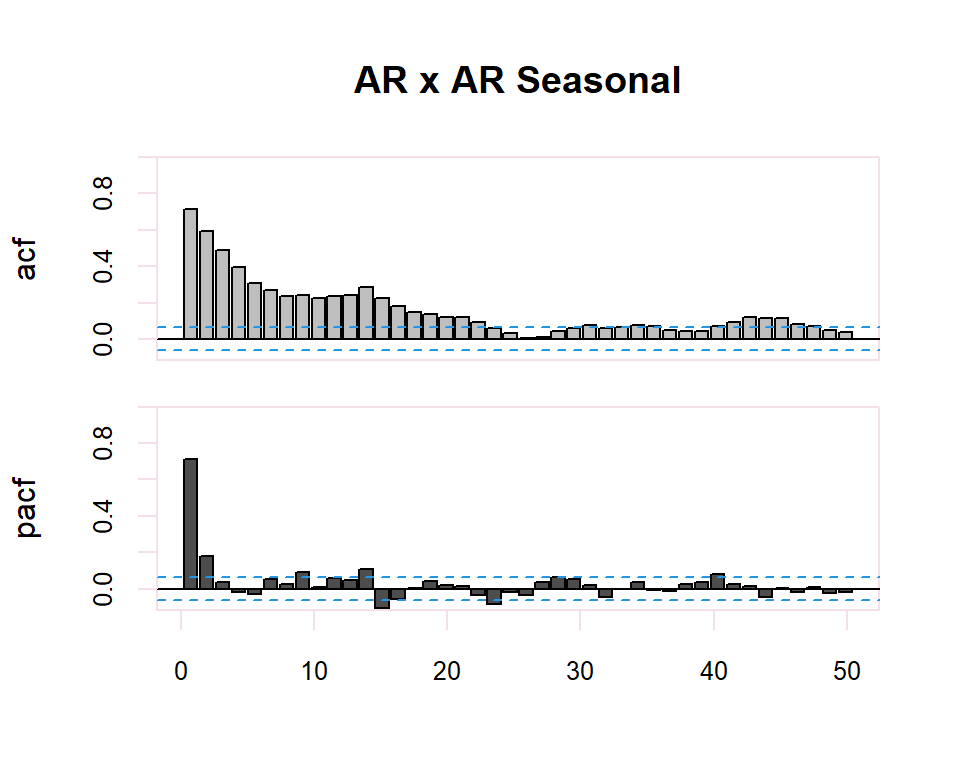
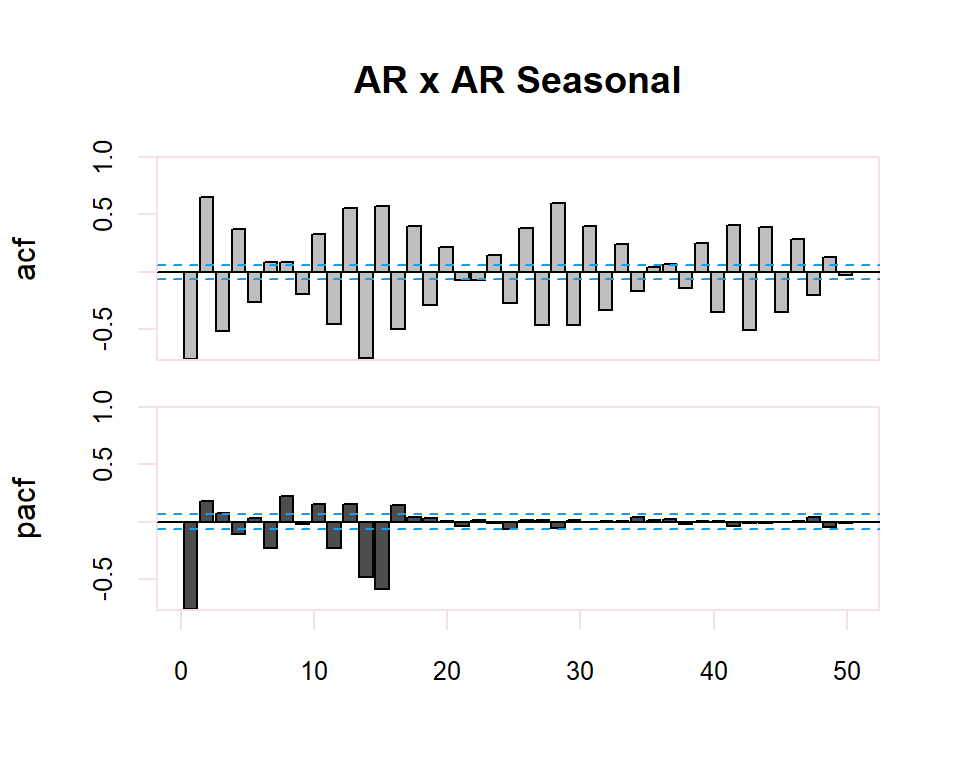
20.1.2 ARMA y ARMA Seasonal
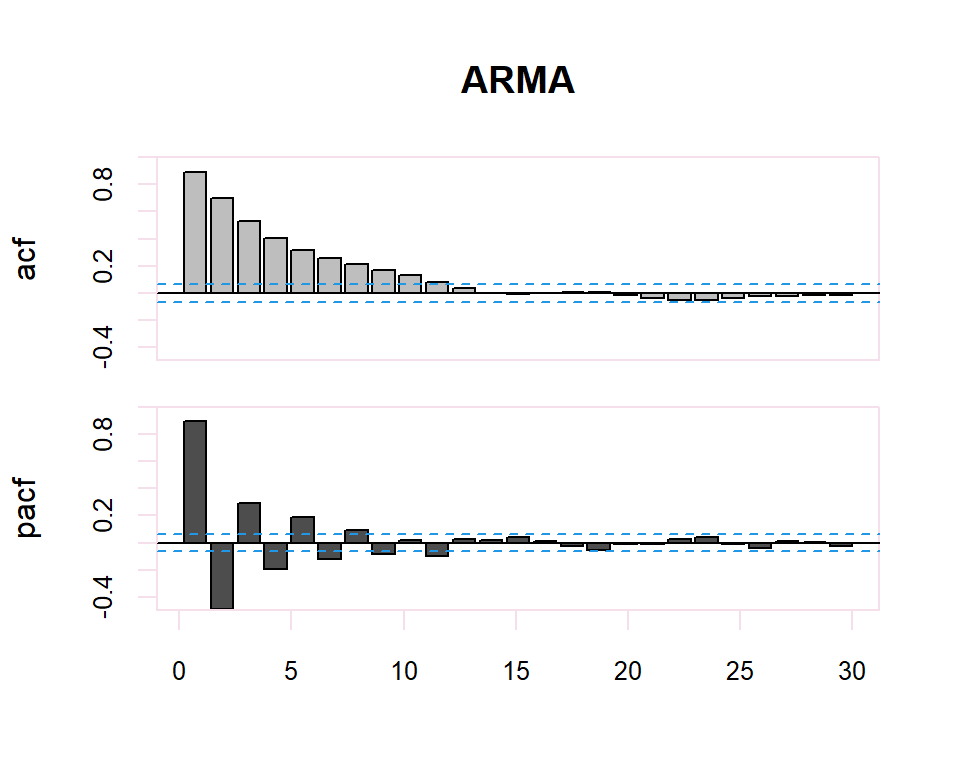
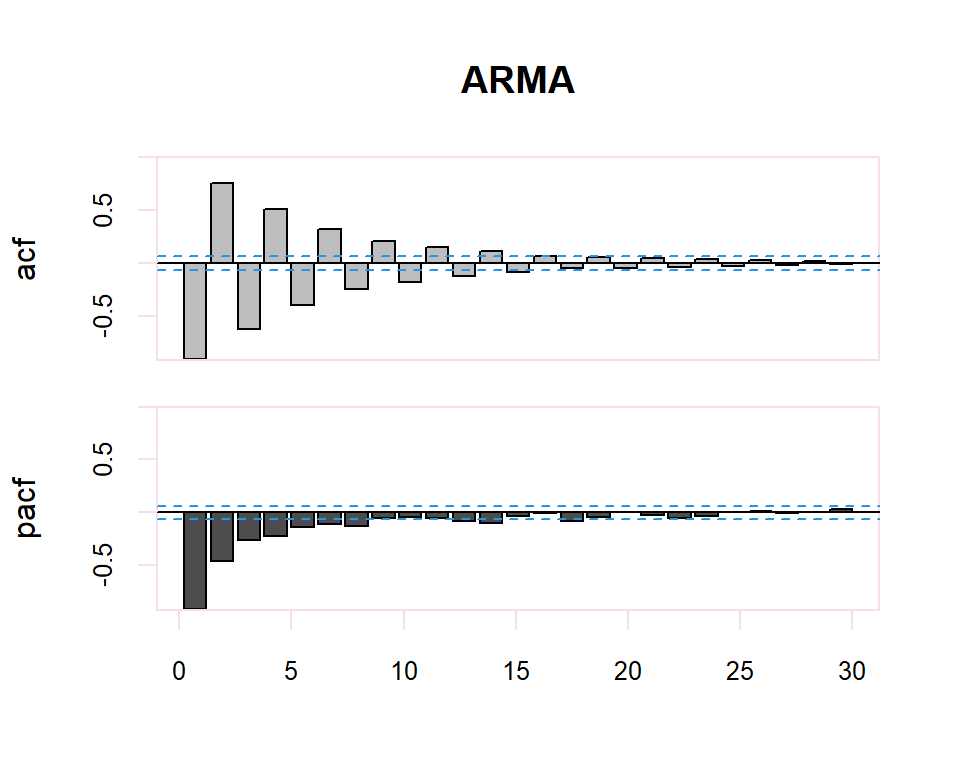
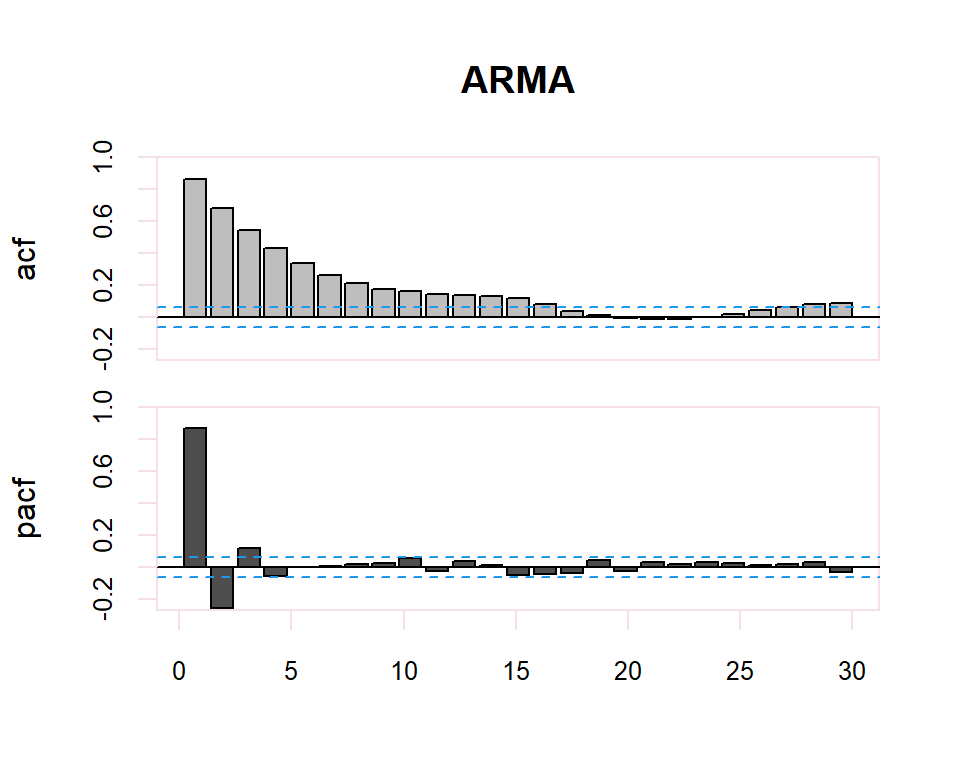
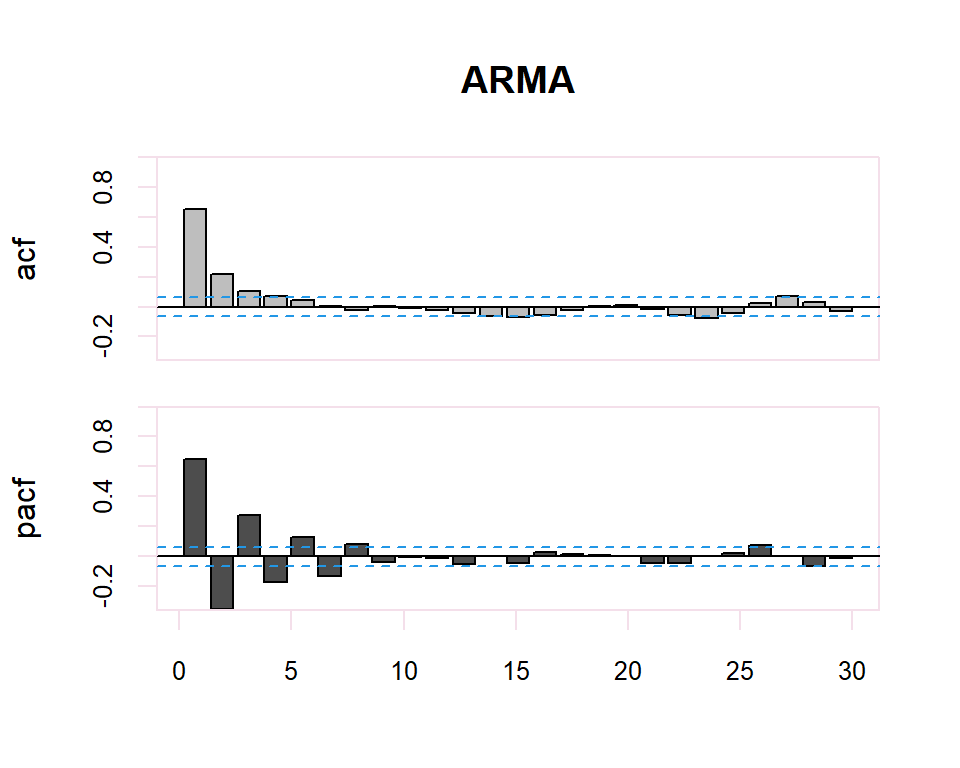
| FAS (ACF) | FAP (PACF) | |
|---|---|---|
| AR(p) | Muchos coeficientes no nulos (Funciones exponenciales y/o sinusoidales). | Primeros p no nulos, resto 0 |
| MA(q) | Primeros q no nulos, resto 0 | Muchos coeficientes no nulos (Funciones exponenciales y/o sinusoidales) |
| ARMA (p,q) | Muchos coeficientes no nulos (Funciones exponenciales y/o sinusoidales) | Muchos coeficientes no nulos (Funciones exponenciales y/o sinusoidales) |
El proceso de identificación es totalmente subjetivo ya que se trata de determinar si la FAC o FACP decerece o se corta. Sin embargo, se disponen de herramientas que facilitan esta tarea. Por ejemplo, para determinar si la estimación de un coeficiente de correlación simple o parcial es significativamente distinto de cero se dispone de una región de confianza determinada por el intervalo \(\pm \dfrac{2}{N}\) donde \(N\) es el número de observaciones en la serie.
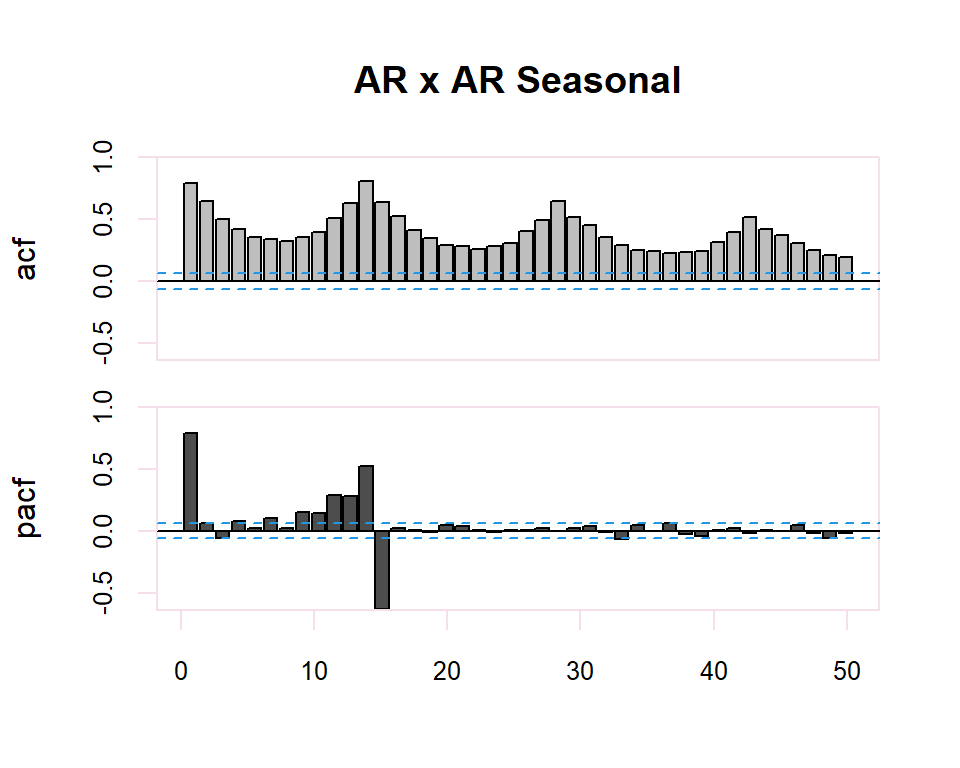
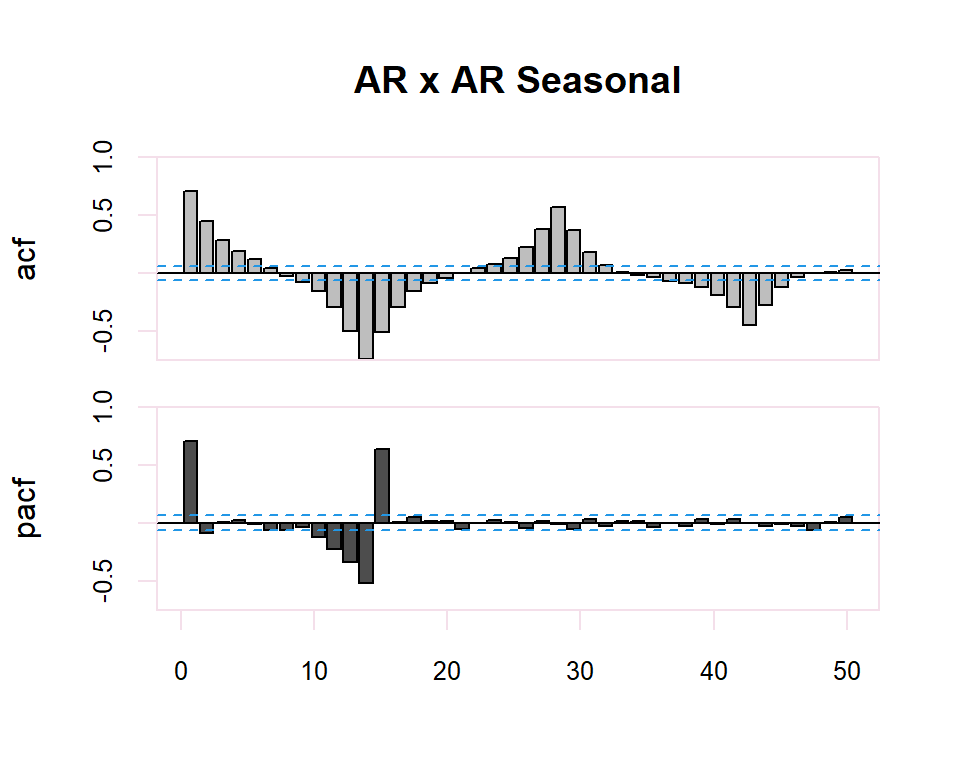
Finalmente, en el caso de existir estacionalidad en la serie temporal, se realizará la identificación de la parte regular observando los primeros retardos del correlograma y de la parte estacional observando los múltiplos de la frecuencia de observación \(s\), de la serie. En el caso estacional se seguirán también los patrones de la tabla anterior.