23.1 Definición

Un proceso estocástico \(( Y_{t} )\) es no estacionario cuando las propiedades estadísticas de al menos una secuencia finita \(Y_{t_1}, Y_{t_2}, \ldots, Y_{t_n} ; n \geq 1;\) de componentes de \(Y_{t}\), son diferentes de la secuencia \(Y_{t_{1+h}}, Y_{t_{2+h}}, \ldots, Y_{t_{n+h}}\) para al menos un número entero h>0.

Muchas series temporales no pueden considerarse generadas por procesos estocásticos estacionarios (es decir, son series no estacionarias), porque presentan cierta tendencia clara en su evolución temporal (de manera que no presentan afinidad hacia algún valor constante en el tiempo), porque su dispersión no es constante, porque son estacionales, o por varias combinaciones de estos motivos.

No obstante, muchas series temporales no estacionarias se pueden transformar de forma adecuada para obtener series de aspecto estacionario, que pueden ser utilizadas como punto de partida para elaborar en la práctica modelos \(\operatorname{ARMA}(p, q)\).

Para convertir una serie no estacionaria en otra estacionaria, suelen emplearse dos tipos de transformaciones:

• Para estabilizar su dispersión (es decir, para inducir estacionariedad en varianza) y
• Para estabilizar su nivel (es decir, para eliminar su tendencia o para inducir estacionariedad en media).

23.1.1 No estacionariedad en Varianza

Sea \(\left( Y_{t} \right)\) un proceso estocástico no estacionario tal que

\[ \mu_{t} \equiv \mathrm{E}\left[Y_{t}\right] \text { y } \sigma_{t}^{2} \equiv \operatorname{Var}\left[Y_{t}\right] \] existen y dependen de \(t\) (por lo que no son constantes). Si

\[ \sigma_{t}^{2}=\sigma^{2} \times h\left(\mu_{t}\right)^{2} \]

donde \(\sigma^{2}>0\) es una constante y \(h(\cdot)\) es una función real tal que \(h(\cdot) \neq 0\) para cualquier valor de \(\mu_{t}\), entonces una transformación estabilizadora de la varianza de \(\left(Y_{t}\right)\) es cualquier función real \(g(\cdot)\) tal que \(g^{\prime}(\cdot)=\frac{1}{h(\cdot)}\) para cualquier valor de \(\mu_{t} .\)

23.1.1.1 Estabilización de la Dispersión - Transformación Logarítmica

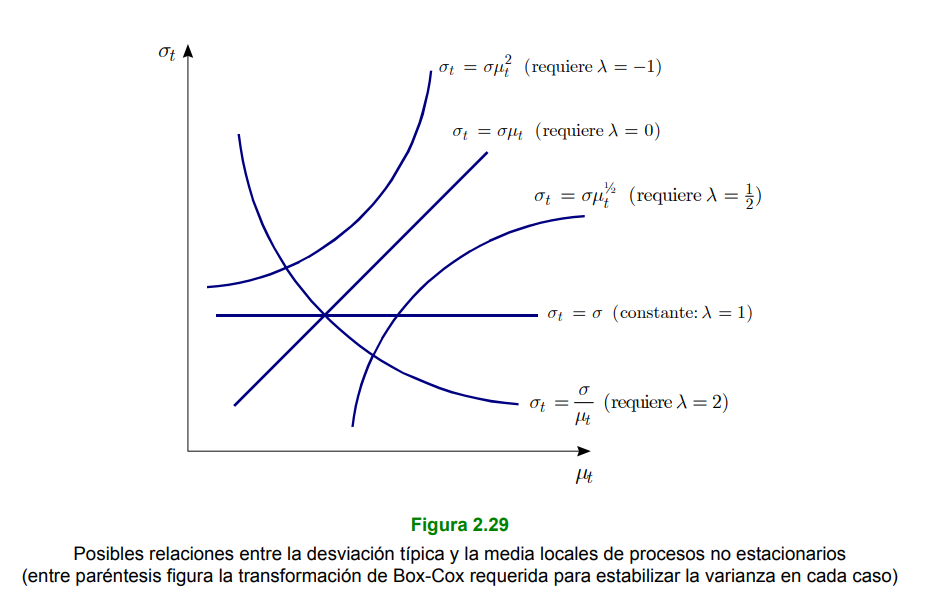
Cuando la dispersión de una serie temporal no estacionaria \(Y_{t}(t=1, \ldots, N)\) no es constante porque su desviación típica local es aproximadamente proporcional a su nivel local, la dispersión de la serie transformada logarítmicamente \(\dot{Y}_{t}=\ln Y_{t} (t=1, \ldots, N)\) suele ser razonablemente estable.

23.1.2 No estacionariedad en Media

Un proceso estocástico \(\left( Y_{t} \right)\) es integrado de orden \(d(d \geq 0\) entero), o \(\mathbf{I}(\boldsymbol{d})\), si y sólo si el proceso \(\left(\nabla^{d} Y_{t}\right)\) sigue un modelo \(\operatorname{ARMA}(p, q)\) estacionario e invertible. En tal caso, suele escribirse

\[\left( Y_{t}\right ) \sim \mathrm{I}(d)\].

23.1.2.1 Estabilización del Nivel Medio General - Diferenciación Regular

El operador diferencia regular de orden \(d\left(d \geq 1\right.\) entero) se representa con el símbolo \(\nabla^{d}\) \(\left(\right.\) a veces \(\left.\Delta^{d}\right)\) y se define como \(\nabla^{d} \equiv(1-B)^{d}\) (donde \(B\) es el operador de retardo), de manera que \[ \nabla X_{t} \equiv X_{t}-X_{t-1}, \nabla^{2} X_{t} \equiv X_{t}-2 X_{t-1}+X_{t-2}, \ldots \] donde \(X_{t}\) es una variable (real o aleatoria) referida a un momento \(t\) determinado.

23.1.2.2 Desestacionalización - Diferenciación Estacional

El operador diferencia estacional de periodo \(S\) y orden \(D(D \geq 1\) entero) se representa con el símbolo \(\nabla_{S}^{D}\) (a veces \(\left.\Delta_{S}^{D}\right)\) y se define como \(\nabla_{S}^{D} \equiv\left(1-B^{S}\right)^{D}\) (donde \(B\) es el operador de retardo), de manera que, en particular (cuando \(D=1\) ),

\[ \nabla_{S} Y_{t} \equiv Y_{t}-Y_{t-S} \] donde \(Y_{t}\) es una variable (real o aleatoria) referida a un momento \(t\) determinado.