17.1 El Modelo AR(1)
Un modelo AR(1) se representa por:
\[ y_t=\delta + \phi_1 y_{t-1}+\omega_t \]
Se puede ver como un Modelo de Regresión Lineal Simple, pero hay una gran diferencia: Las variables regresoras no son elegidas por el modelador ni se pueden controlar.
Los supuestos que deben cumplirse son:
- \(\omega_t\) son independientes y se distribuyen como \(N(0,\sigma^2_\omega).\) Los errores siguen una distribución Normal con media cero y varianza constante.
- Las propiedades de \(\omega_t\) son independientes de \(y\).
| Observation | ||||
|---|---|---|---|---|
| Parametro | Estimates | std. Error | t-test | p-valor |
| (Intercept) | 9.19 | 1.82 | 5.05 | <0.001 |
| lag1 | 0.54 | 0.09 | 6.37 | <0.001 |
| Observations | 98 | |||
| R2 / R2 adjusted | 0.297 / 0.290 | |||
Observamos que el coeficiente de Lag 1 es significativamente diferente de 0, por lo que la variable \(y_{t-1}\) es un predictor útil. Sin embargo, el valor es \(R^2\) relativamente bajo, un 29,7%, por lo que no esperamos predicciones muy precisas.
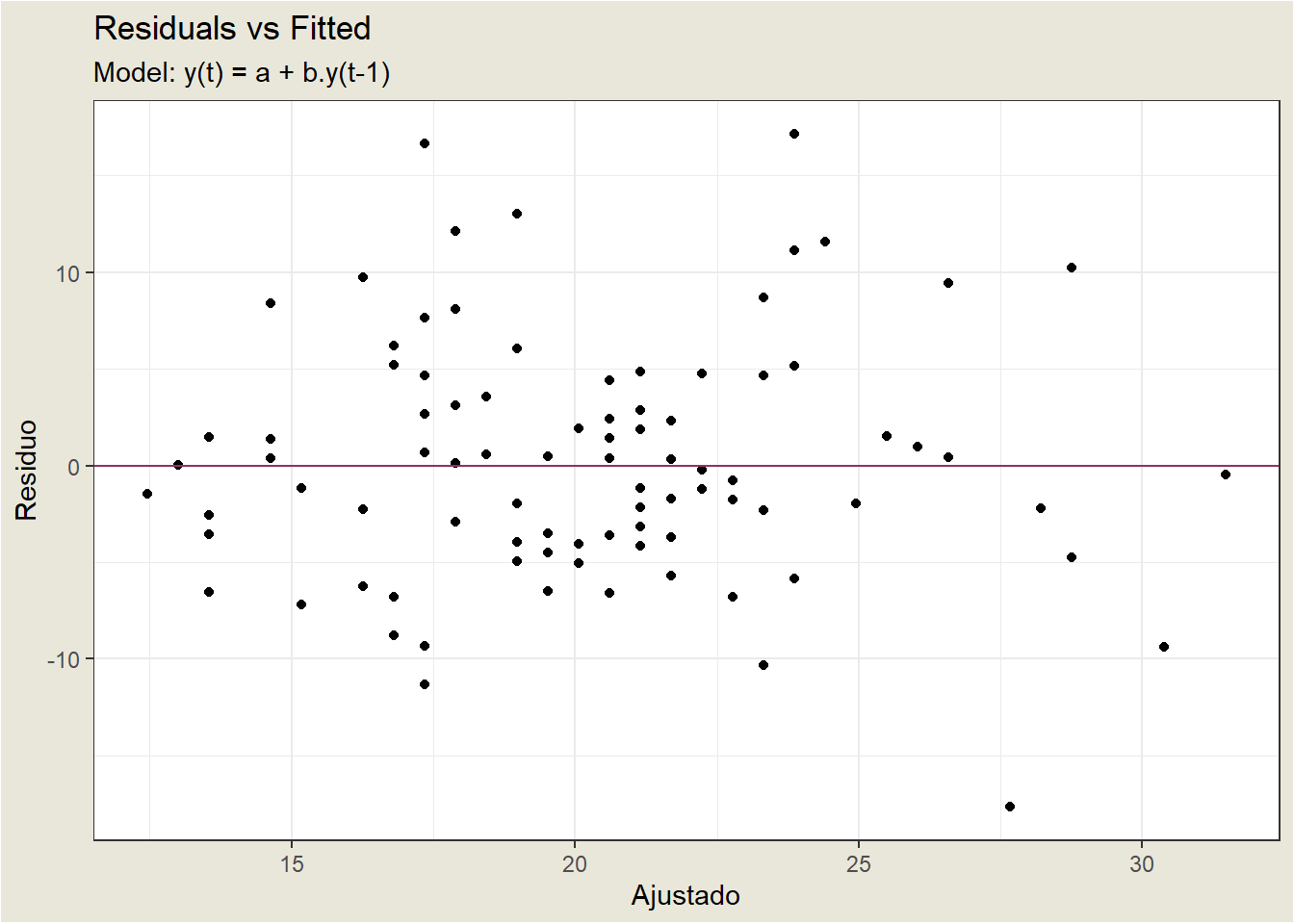
17.1.1 Análisis de Residuos
Continuando con la diagnosis, observaos el gráfico de residuos frente a los valores ajustados (fitted values). Lo ideal para este gráfico es obtener una banda horizontal de puntos. A continuación se muestra un gráfico de los residuos frente a los valores predichos para nuestro modelo estimado. No muestra ningún problema grave, salvo un posible valor atípico en la observación 28.
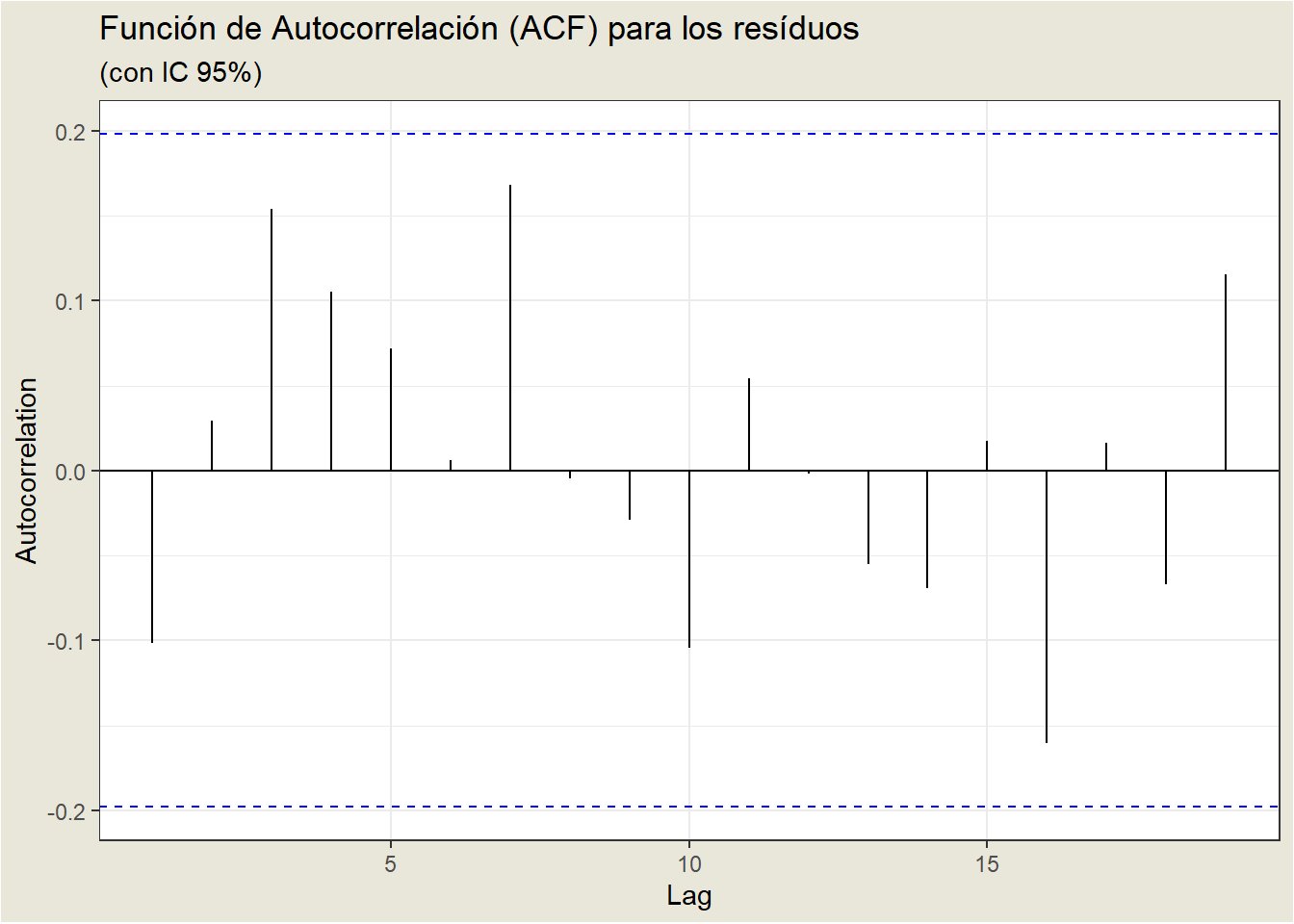
La función de autocorrelación muestral (ACF) de una serie proporciona las correlaciones entre la serie \(x_t\) y los valores rezagados (lagged values) de la misma para rezagos de 1, 2, 3, etc. Los valores retardados pueden escribirse como \(x_{t-1}, x_{t-2}, x_{t-3}\), y así sucesivamente. La ACF proporciona correlaciones entre \(x_t\) y \(x_{t-1}\), \(x_t\) y \(x_{t-2}\), etc.
La ACF puede utilizarse para identificar la posible estructura de los datos de las series temporales. Esto puede ser una tarea complicada, ya que a menudo no hay una interpretación clara de la función de autocorrelación de una muestra.
La ACF de los residuos de un modelo también es útil. Lo ideal es que en la ACF de los residuos no se observen correlaciones significativas para ningún retardo.
A continuación se muestra la ACF de los residuos para el ejemplo de los terremotos, en el que utilizamos un modelo AR(1). El lag"_ (intervalo de tiempo entre las observaciones) se muestra en el eje horizontal, y la autocorrelación en el eje vertical. Las líneas horizontales indican los límites de significación estadística. Podemos decir que el ACF de los residuos es bueno ya que ninguna correlación es significativa; lo que necesitamos para los residuos.