7 Introducción

La regresión logística se utiliza para modelar la probabilidad de una variable cualitativa binaria en función de una o más variables independientes. Se utiliza en problemas de clasificación.

La variable output es Binaria o Dicotómica:

$$Y = \begin{cases} 1 & \text{si presente | verdadero | éxito} ,\\ 0 & \text{si ausente | falso | fracaso} \end{cases}$$

Ejemplos

• ¿Votó en las últimas elecciones? Si/No
• ¿Renovará la suscripción? Si/No
• ¿Presentará una reclamación? Si/No
• ¿Cambiará de móvil? Si/No
• ¿Tiene ojos azules? Si/No

Nuestro objetivo es especificar un modelo, $f(\cdot),$ que relacione la variable dependiente, $Y,$ con una o más variables independientes, $X_1,\ldots, X_K.$:

$$Y = f(X) = f(X_1,\ldots, X_K)$$

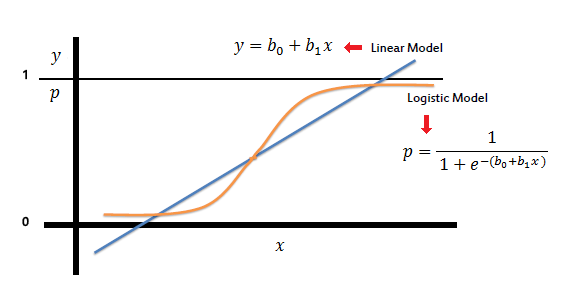
Cuando $f(X)$ es una regresion lineal simple tenemos: $y_i = \beta_0 +\beta_1x_{i} +\epsilon_i$.

Decimos que el valor esperado de la variable dependiente $Y,$ dado el valor de la variable independiente $x$ está dado por $E[Y|x]=\beta_0 +\beta_1x_{1}.$ Luego $E[Y|x] \in (-\infty,+\infty)$

Fuente: Aquí

Conceptos importantes

• Probabilidad: si la probabilidad de éxito es $p=0.8$, la probabilidad de fracaso es $1-p=0.2$

• Odds: Es el ratio entre probabilidad de éxito y la probabilidad de fracaso. $\operatorname{odds}= \dfrac{p}{1-p}=\dfrac{0.8}{0.2}=4.$ Es decir, los odds de éxito son 4 a 1.

• Odds Ratio: Es el ratio entre Odds. $\operatorname{OR}= \dfrac{\operatorname{odds}_1}{\operatorname{odds}_2}=\dfrac{\frac{p_1}{1-p_1}}{\frac{p_2}{1-p_2}}$