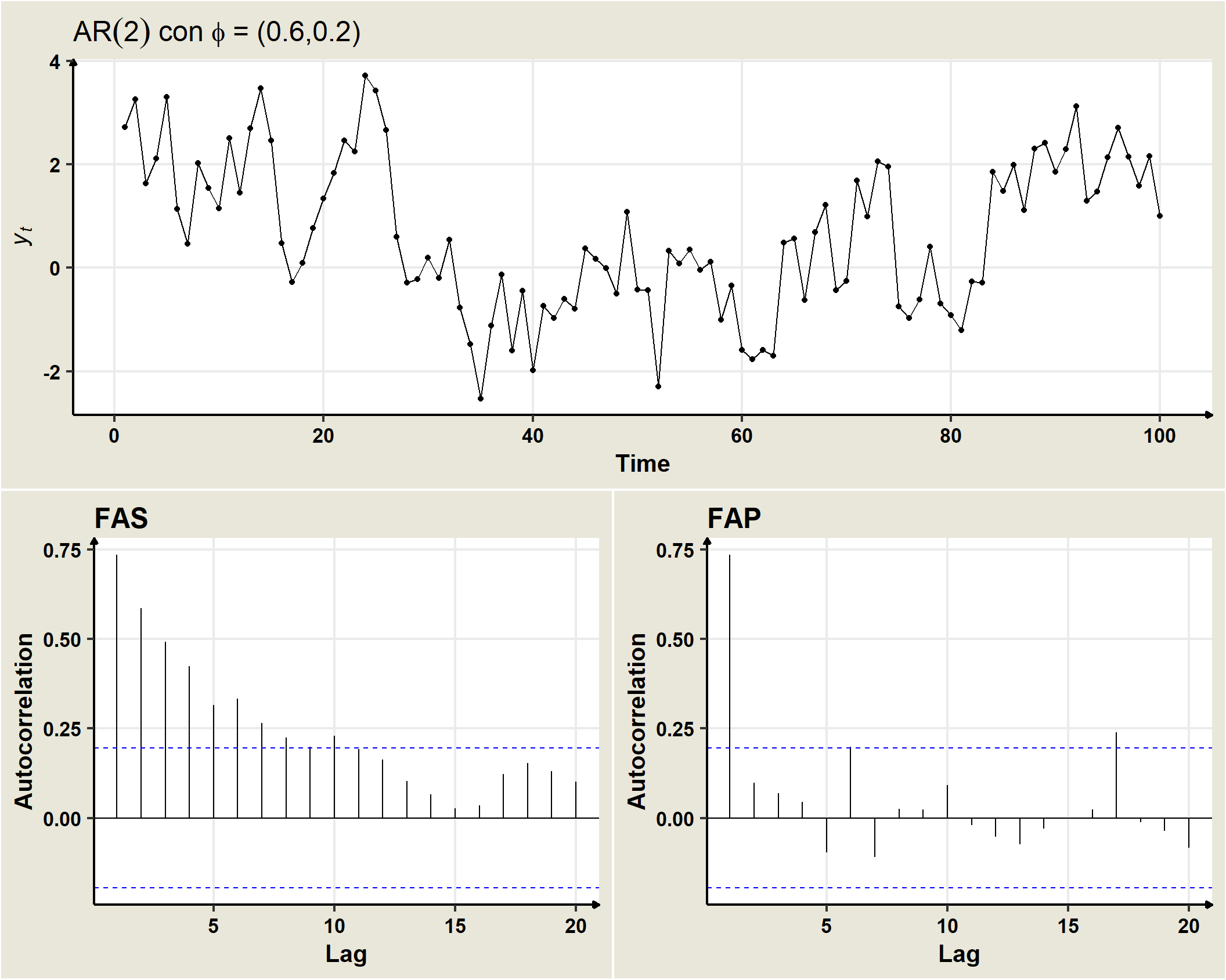
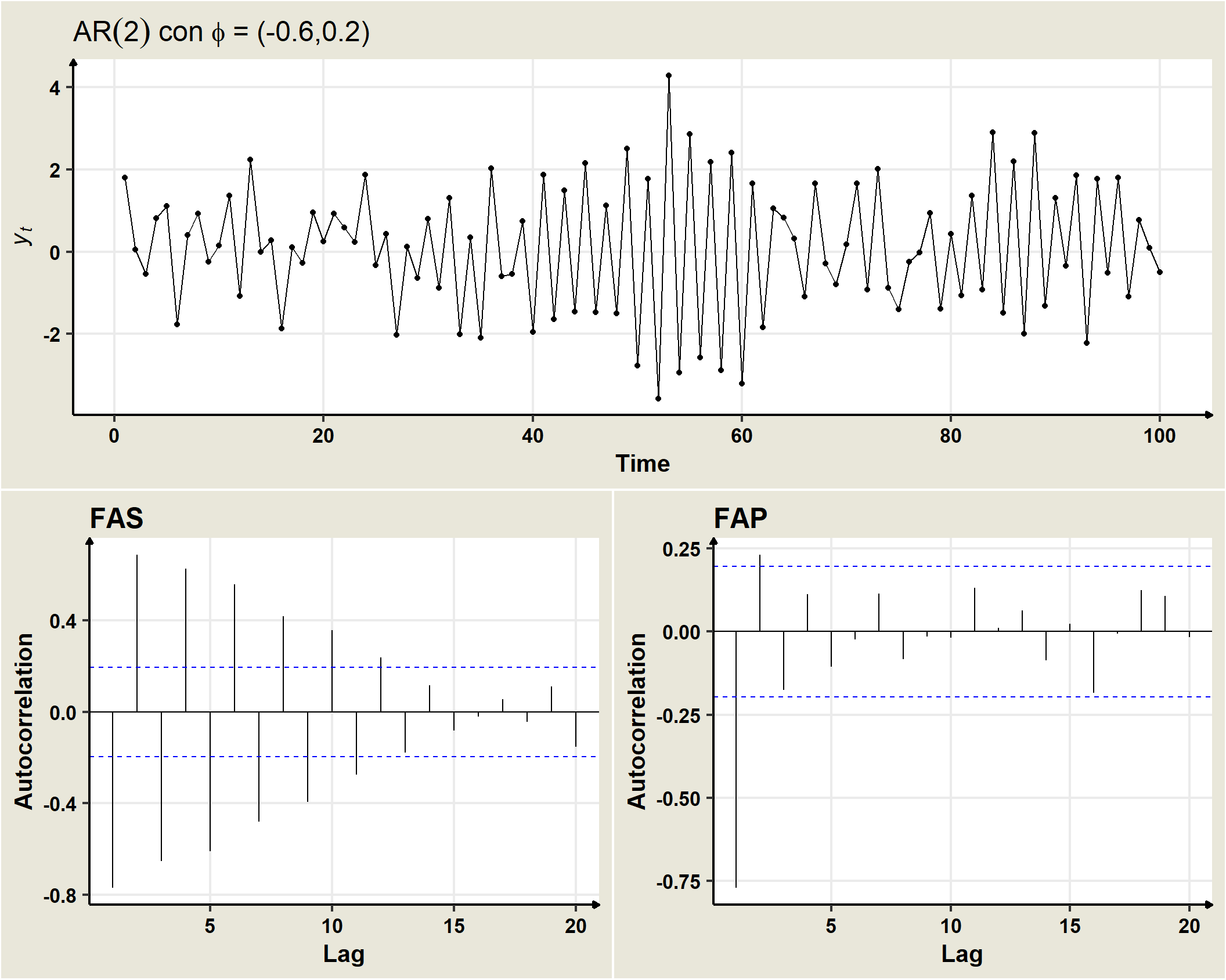
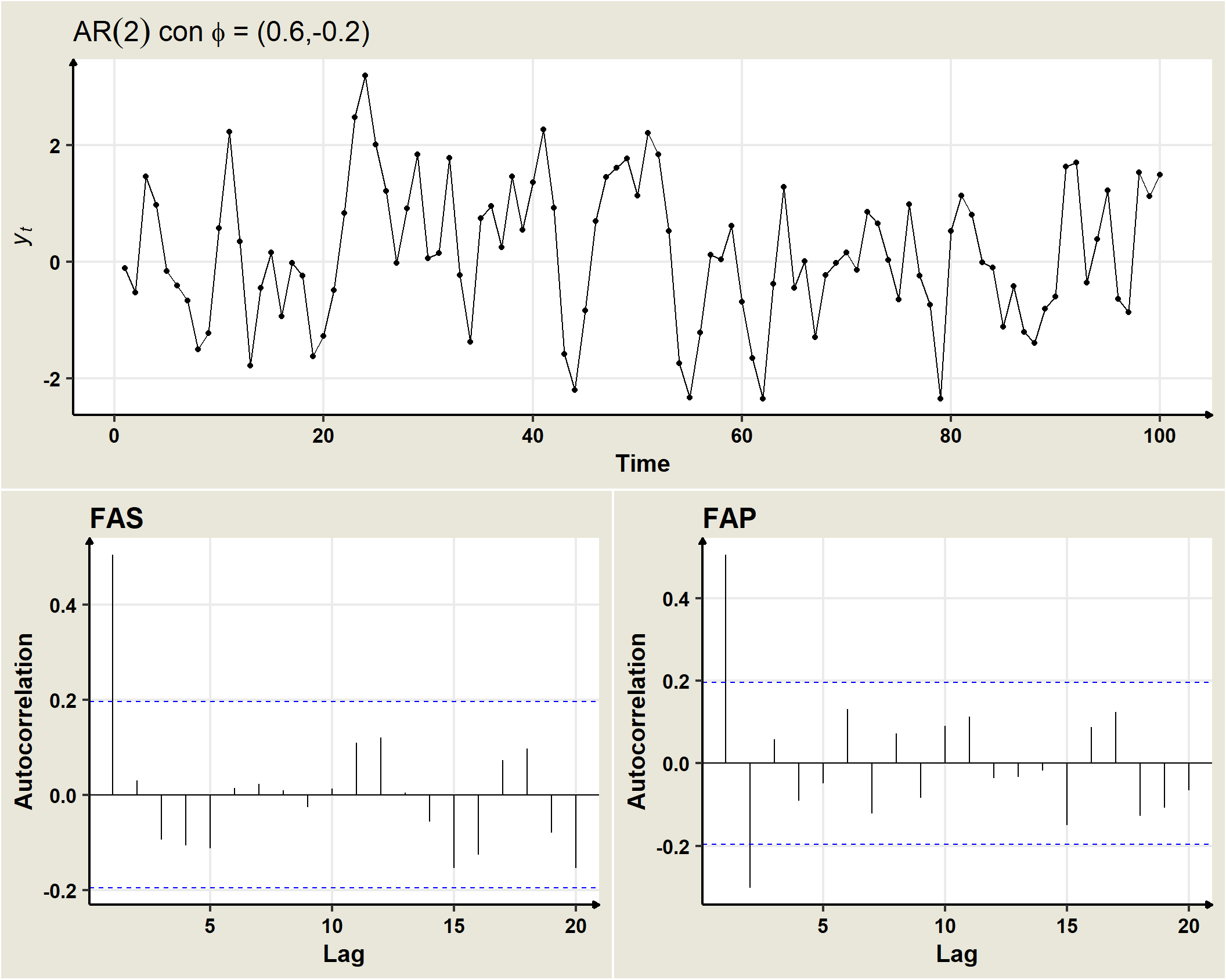
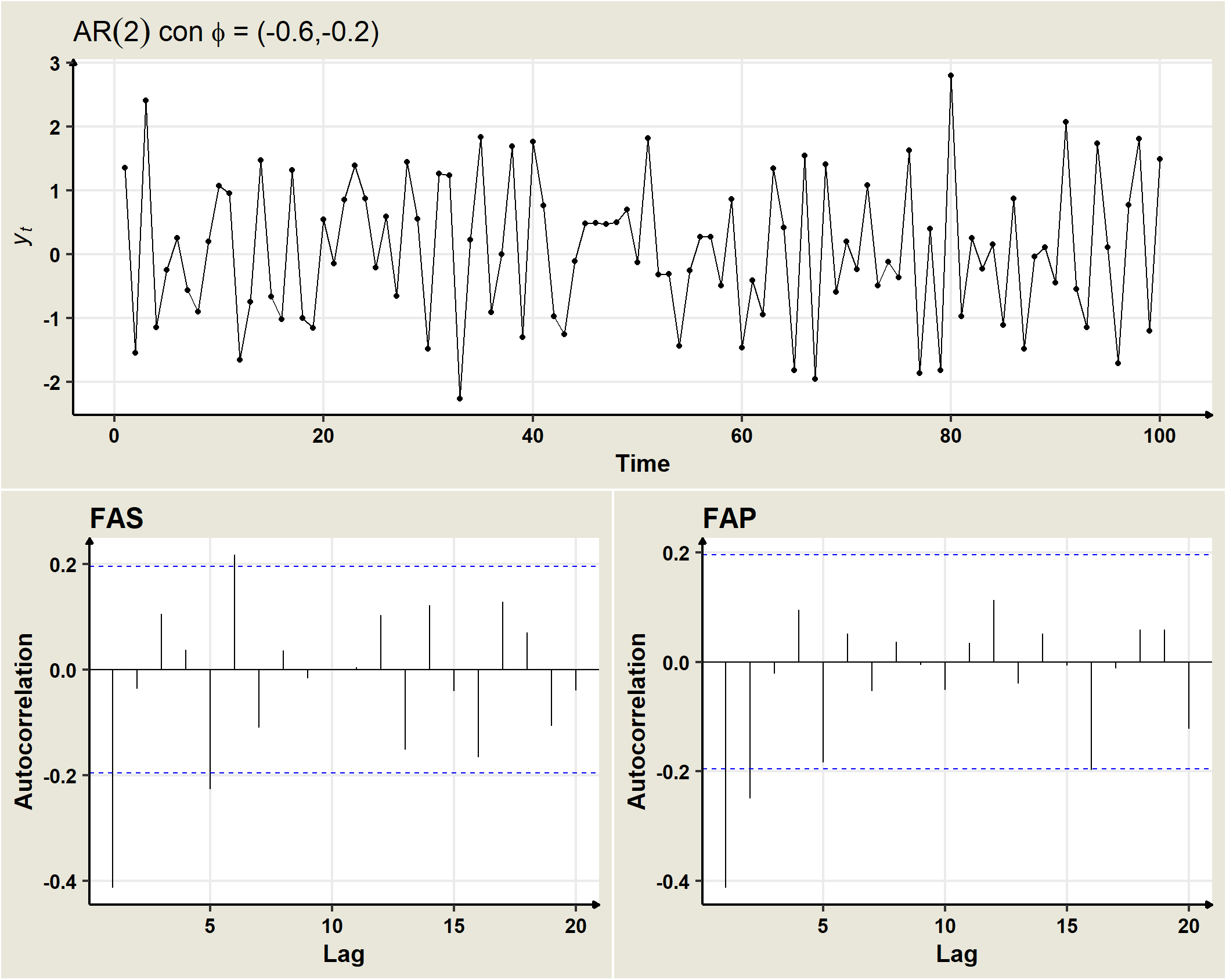
19.5 AR(2)

Modelo autorregresivo de orden 2: AR(2)

Un proceso AR(2) se genera a partir de:

Yt=δ+ϕ1Yt−1+ϕ2Yt−2+ωt donde wt es un ruido blanco con media cero y varianza σ2ω,→ωt∼N(0,σ2ω.


Cuando un proceso estacionario (Yt) sigue un modelo AR(2),

Yt=μ+ϕ1Yt−1+ϕ2Yt−2+ωt con ϕ2+ϕ1<1,ϕ2−ϕ1<1,|ϕ2|<1 (ver 2.3.1) y(ωt)∼IID(0,σ2ω), puede comprobarse lo siguiente:

  • Media: μY=μ1−ϕ1−ϕ2ρk=ϕ1ρk−1+ϕ2ρk−2(k≥1)

  • ACF: ρk=ϕ1ρk−1+ϕ2ρk−2(k≥1)

  • PACF:

ϕkk={ϕ1/(1−ϕ2) si k=1ϕ2 si k=20 para todo k>2.

  • Varianza:

σ2Y=σ2A1−ϕ1ρ1−ϕ2ρ2=[1−ϕ21+ϕ2][σ2A(1−ϕ1−ϕ2)(1+ϕ1−ϕ2)]

Más detalles

Si el proceso es estacionario en media y varianza entonces se verificará que E[Yt]=E[Yt−1] y $Var(Y_t) = Var(Y_{t-1}), t , $ de forma que:

E[Yt]=E[Yt−1]=μ=δ+ϕ1μ+ϕ2μ→μ=δ1−ϕ1−ϕ2 y

Var(Yt)=Var(Yt−1)=γ0=ϕ21γ0+ϕ22γ0+σ2ω→γ0=σ2ω1−ϕ21−ϕ22

donde ϕ1+ϕ2≠1.

Además:

cov(Yt,Yt−1)=cov(Yt−1,Yt)=E[(Yt−μ)(Yt−1−μ)]=E[ytyt−1]=γ1γ1=E(yt−1yt)=E[yt−1(ϕ1yt−1+ϕ2yt−2+ωt)]=ϕ1γ0+ϕ2γ1γ2=E(yt−2yt)=E[yt−2(ϕ1yt−1+ϕ2yt−2+ωt)]=ϕ1γ1+ϕ2γ0…γk=E(yt−kyt)=E[yt−k(ϕ1yt−1+ϕ2yt−2+ωt)]=ϕ1γk−1+ϕ2γk−2

donde yt=(Yt−μ).