17.2 Propiedades del Modelo AR(1)

Como paso previo, definimos una serie estacionaria. Para que un ACF tenga sentido, la serie debe ser una serie débilmente estacionaria. Esto significa que la autocorrelación para cualquier retardo concreto es la misma independientemente de dónde nos encontremos en el tiempo.

Series estacionarias

Una serie $y_t$ es (débilmente) estacionaria si satisface las siguientes propiedades:

• La media $E[y_t]$ es la misma para todo $t$
• La varianza de $y_t$ es la misma para todo $t$
• La covarianza (y la correlación) entre $y_t$ e $y_{t-1}$ es la misma para todo $t$

Función de Autocorrelación (ACF)

Sea $y_t$ es el valor de una serie temporal en el instante $t$.

La ACF de una serie temporal proporciona la correlación entre $y_t$ e $y_{t-h}$ para $h=1,2,3,\ldots$.

La autocorrelación (teórica) entre $y_t$ e $y_{t-h}$ es:

$$\dfrac{\text{Covariance}(y_t, y_{t-h})}{\text{Std.Dev.}(y_t)\text{Std.Dev.}(y_{t-h})} = \dfrac{\text{Covariance}(y_t, y_{t-h})}{\text{Variance}(y_t)}$$

$$\rho_{h} = \frac{\sum\limits_{t=h+1}^T (y_{t}-\bar{y})(y_{t-h}-\bar{y})} {\sum\limits_{t=1}^T (y_{t}-\bar{y})^2},$$

El denominador es la varianza porque la desviación típica de una serie estacionaria es la misma en todo momento. Es decir $\text{Std.Dev.}(y_t) = \text{Std.Dev.}(y_{t-h}), \forall h$

La última propiedad de una serie (débilmente) estacionaria dice que el valor teórico de la autocorrelación de un determinado retardo es el mismo en toda la serie. Una propiedad interesante de una serie estacionaria es que teóricamente tiene la misma estructura hacia delante que hacia atrás.

Muchas series estacionarias tienen patrones ACF reconocibles. Sin embargo, la mayoría de las series que encontramos en la práctica son no estacionarias.

Una tendencia ascendente continua, por ejemplo, es una violación del requisito de que la media sea la misma para toda la serie. Los patrones estacionales distintos también violan ese requisito. Por lo tanto, es bastante común aplicar técnicas para tratar las series no estacionarias.

17.2.1 Propiedades de un AR(1)

Como establecido anteriormente, un modelo AR(1) se representa por:

$$\begin{equation} y_t=\delta + \phi_1 y_{t-1}+\omega_t \end{equation}$$

Los supuestos que deben cumplirse son:

1. $\omega_t$ son independientes y se distribuyen como $N(0,\sigma^2_\omega).$ Los errores siguen una distribución Normal con media cero y varianza constante.
2. Las propiedades de $\omega_t$ son independientes de $y$.
3. La serie $y_1, y_2, \ldots$ es (débilmente) estacionaria.En el caso del AR(1) este supuesto implica que $|\phi_1|<1.$

Las fórmulas de la media, varianza y ACF de una serie temporal que sigue un proceso AR(1) son:

• La media de $y_t$

$$\begin{equation} E(y_t)=\mu = \dfrac{\delta}{1-\phi_1} \end{equation}$$

• La varianza de $y_t$

$$\begin{equation} \text{Var}(y_t) = \dfrac{\sigma^2_w}{1-\phi_1^2} \end{equation}$$

• La correlación entre observaciones separadas por $h$ períodos de tiempo es

$$\begin{equation} \rho_h = \phi^h_1 \end{equation}$$

$\rho_h$ define el ACF teórico para serie temporal con un modelo AR(1).

Importante:

$\phi_1$ es la pendiente en el modelo AR(1) y también es la autocorrelación del lag 1.

17.2.2 Propiedades de un AR(1)

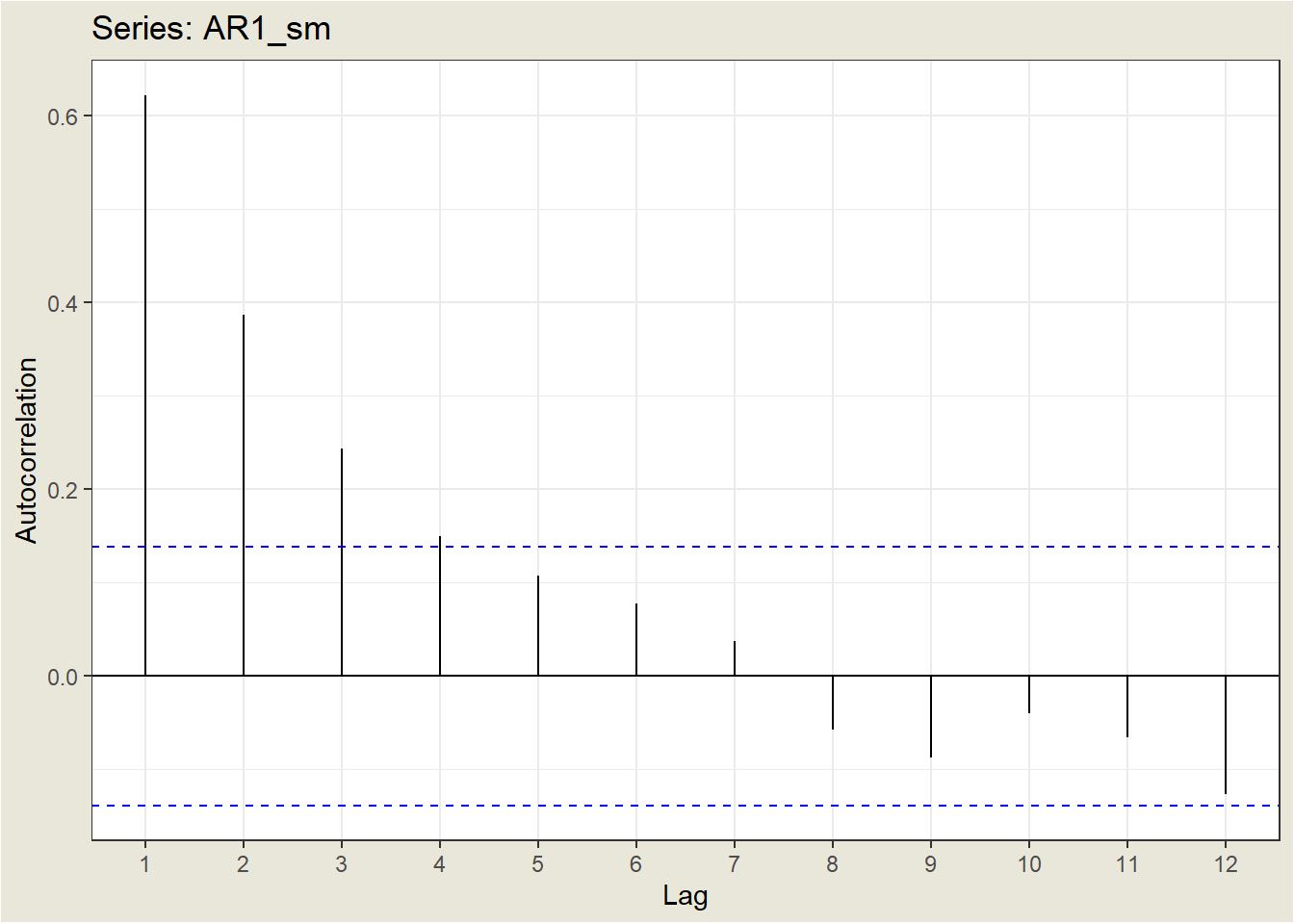
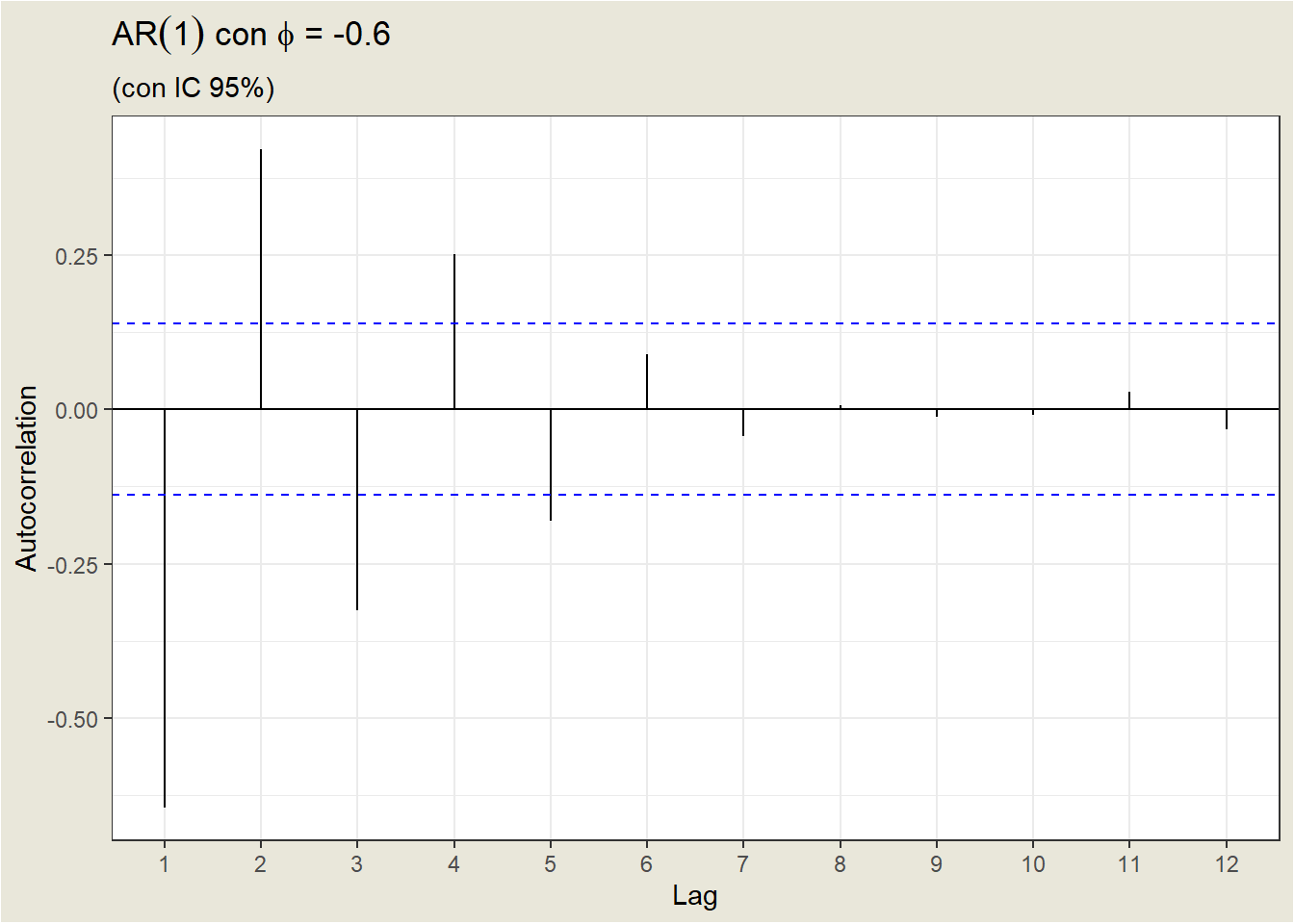
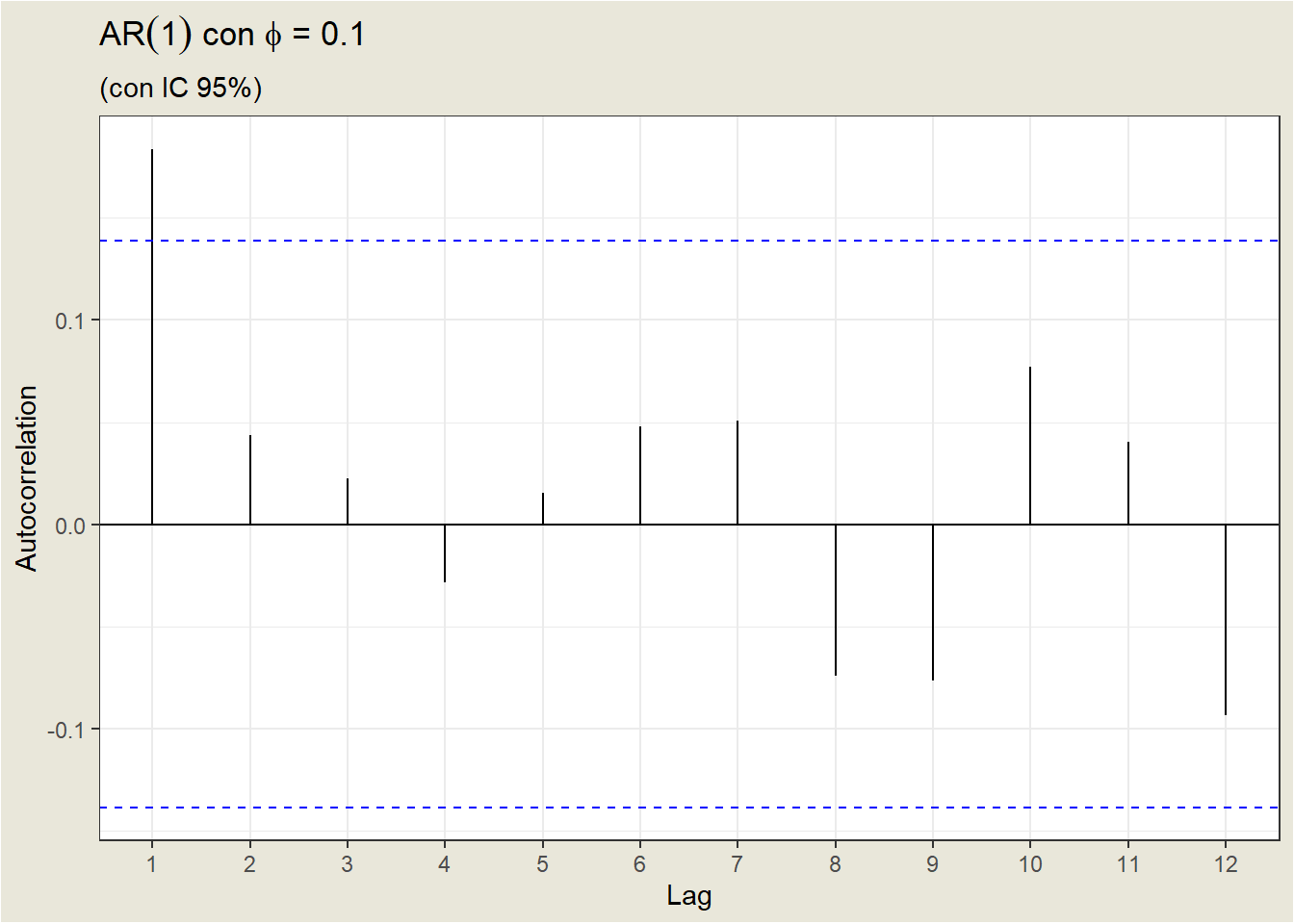
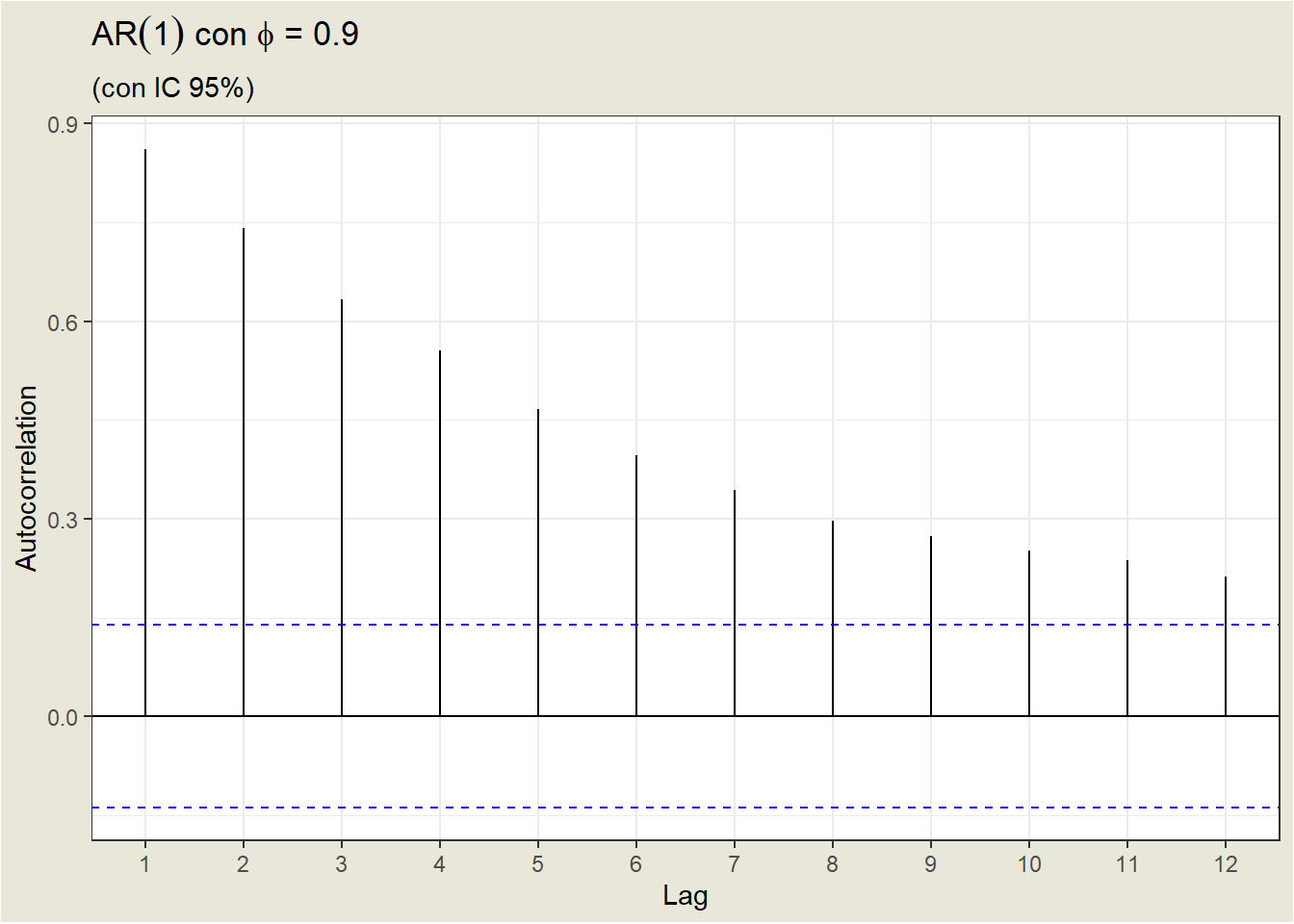
Dependiendo del valor de $\phi_1$, la ACF define un patrón distinto para las autocorrelaciones.

• Para un valor positivo de $\phi_1$, la ACF disminuye exponencialmente hasta 0 a medida que aumenta el retardo.

• Para un valor negativo de $\phi_1$, el ACF también decae exponencialmente hasta 0 a medida que aumenta el retardo, pero los signos de las autocorrelaciones alternan entre positivo y negativo.

Veamos el ACF del Ejemplo Terremotos.

Función de Autocorrelacion
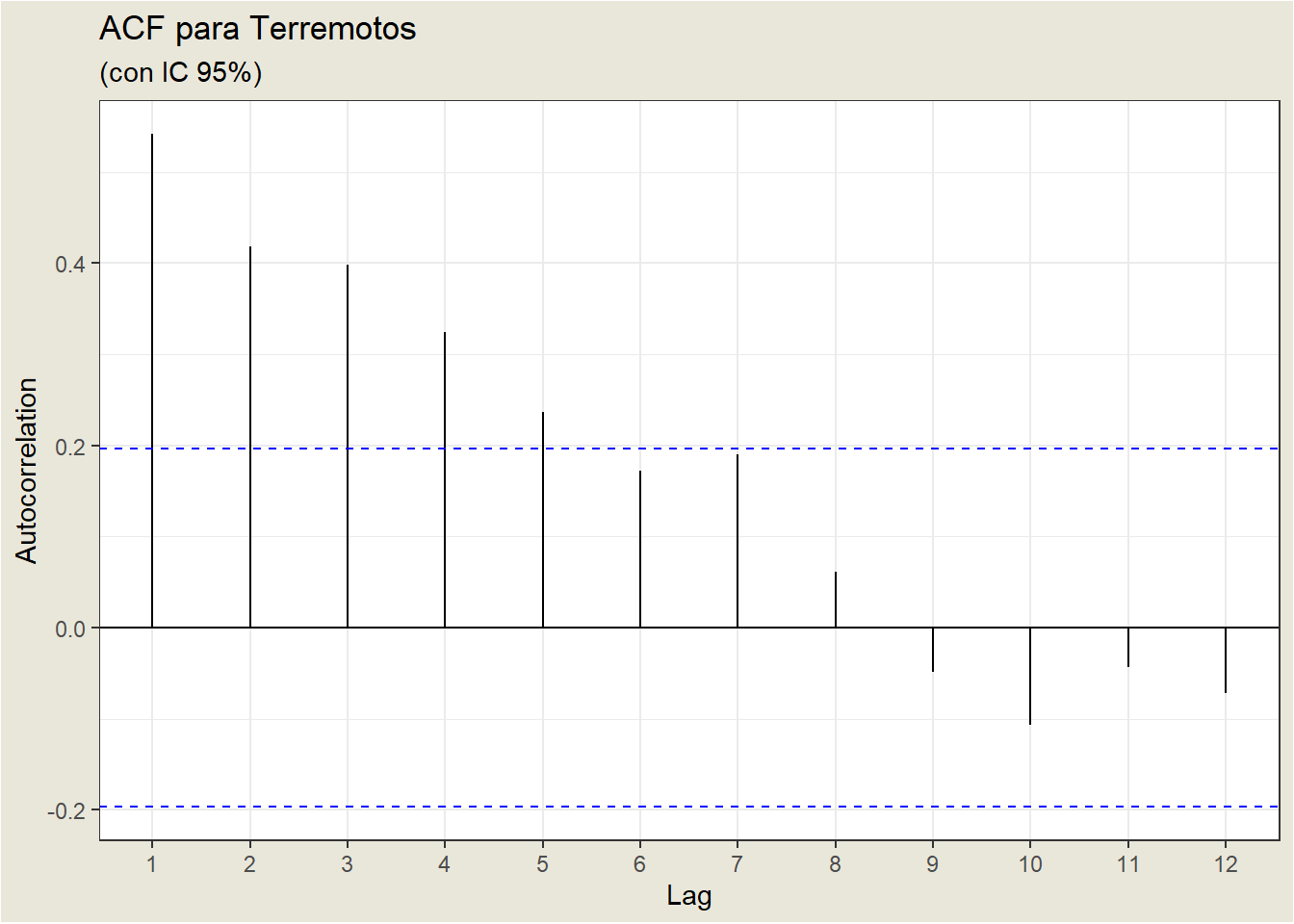
Lag	0	1	2	3	4	5	6	7	8
ACF	1.0000	0.5417	0.4189	0.3980	0.3240	0.2372	0.1718	0.1902	0.0612

Las autorrelaciones muestrales disminuyen, pero no tan rápido como se espera de un AR(1). Por ejemplo, teóricamente, la autocorrelación del retardo 2 para un AR(1) es el cuadrado de la autocorrelación del retardo 1. En el ejemplo, $\rho_2=$ 0.41888 cuando $\rho_1^2=$ 0.2934714

Este caso es un ejemplo de lo que ocurre en la práctica: la ACF muestral rara vez se ajusta a un modelo teórico perfecto. En la mayoría de los casos hay que probar varios modelos y elegir el que mejor se ajusta a los datos.