23.3 Modelos ARIMA

Un proceso estocástico $\left(Y_{t}\right)$ es integrado de orden $d\left(d \geq 0\right.$ entero) si y sólo si $\left(Y_{t}\right)$ sigue un modelo autorregresivo-integrado-media móvil de orden $(p, d, q)$, o $\operatorname{ARIMA}(p, d, q)$ (del inglés AutoRegressive-Integrated-Moving Average), del tipo $$\phi(B) \nabla^{d} Y_{t}=\mu+\theta(B) \omega_{t} \quad \forall t=0, \pm 1, \pm 2, \ldots$$ donde las raíces de las ecuaciones $\phi(x)=0$ y $\theta(x)=0$ están fuera del círculo unitario.

• Paso 1: Determinar $d$
• Paso 2: Determinar $p$ y $q$
• Paso 3: Estimar ARIMA($p,d,q$)
• Paso 4: Previsión

Considerar la siguiente serie temporal

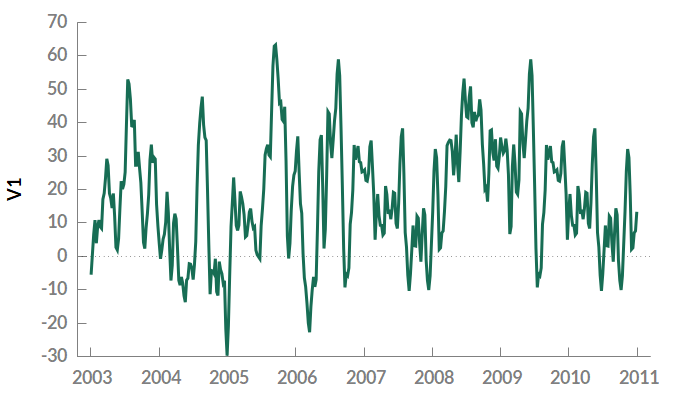
Paso 1: Determinar $d$ para $(Y_t)$

Si $d = 0$ $(Y_t)$ es estacionaria. Si $d = 1$ $(Y_t)$ no es estacionaria y requiere ser diferenciada para ser estacionaria.

Para determinar $d$ se puede utilizar el Test de Dickey Fuller o Test de Raiz Unitaria

• $H_0:$ $(Y_t)$ tiene raiz unitaria
• $H_1:$ $(Y_t)$ no tiene raiz unitaria

En Gretl: Usamos la raiz cúbica de N como Lag order (en este caso, 8)

Paso 2: Determinar $p$ y $q$ para $(Y_t)$

Para determinar $p$ y $q$ hacemos análisis visual del correlograma

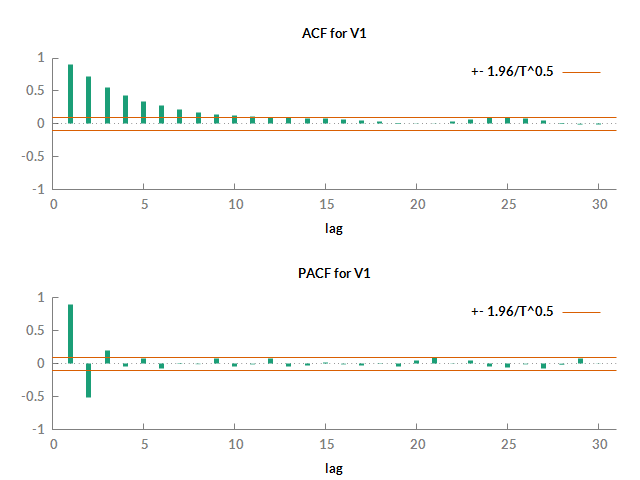
Se observa que tanto FAS (ACF) como FAP (PACF) tienen patrón de decaimiento. El primero decae suavemente, el segundo tiene un patrón oscilante.Este patrón representa $p=1$ y $q=1.$

Paso 3: Estimar ARIMA $p,d,q$ para $(Y_t)$

Como $d=0,$ ajustamos un $ARIMA(1,0,1)$ que es equivalente a $ARMA(1,1)$

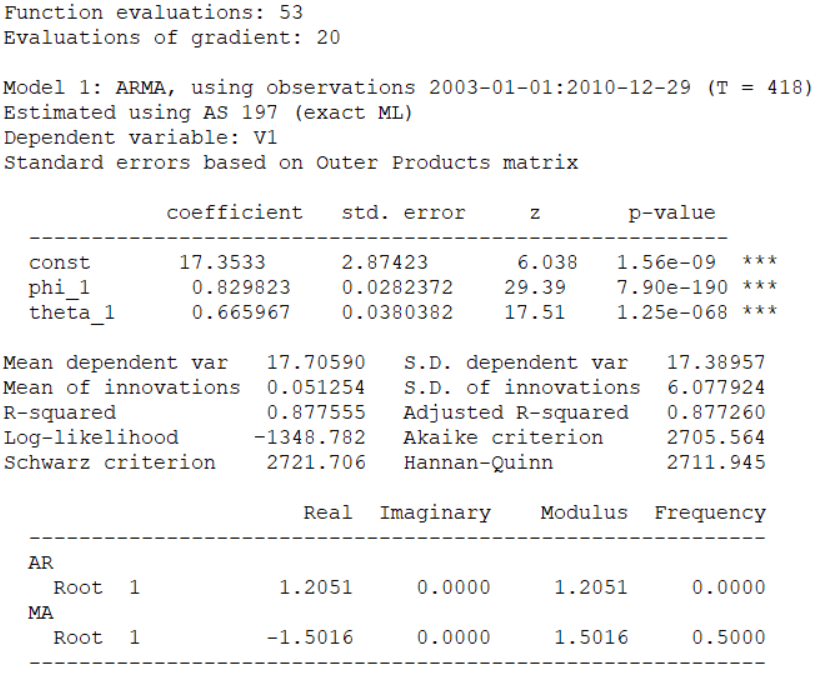
El modelo estimado indica que el coeficiente del término $AR(1)$ es $\phi_1 = 0.83$ y el coeficiente del término $MA(1)$ es $\theta_1 = 0.67,$ ambos estadísticamente significativos.

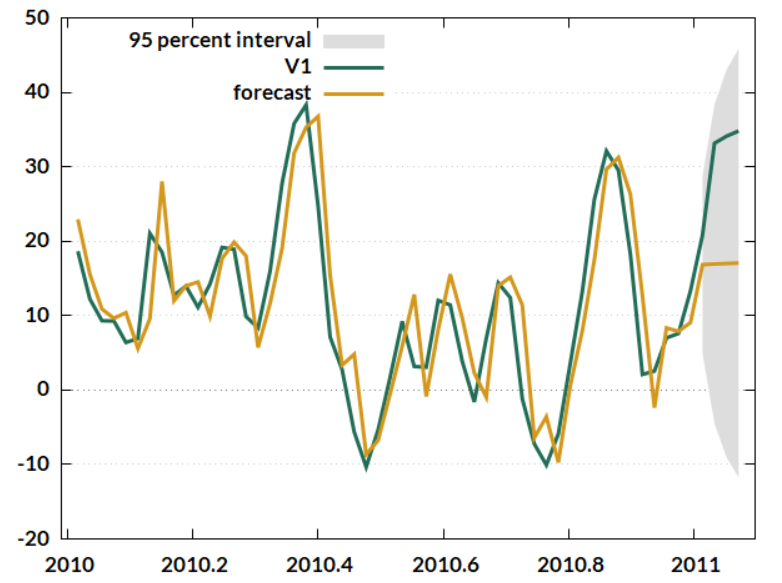
Paso 4: Previsión con ARIMA $p,d,q$ para $(Y_t)$