19.1 Ruido Blanco

Ruido Blancos (white noise) es un proceso estocástico en el que las variables aleatorias que lo forman no están correlacionadas entre sí, tienen esperanza matemática igual a cero y varianza constante e igual a $\sigma^2$.

Los ruidos blancos gaussianos son formados por una sucesión de variables aleatorias con distribución Normal, esperanza cero, varianza constante e incorrelacionadas serialmente entre sí. Es decir, si
$\omega_t \sim N(0,\sigma^2)$ es ruido blanco gaussiano, entonces $cov(\omega_t,\omega_{t+k})=0$

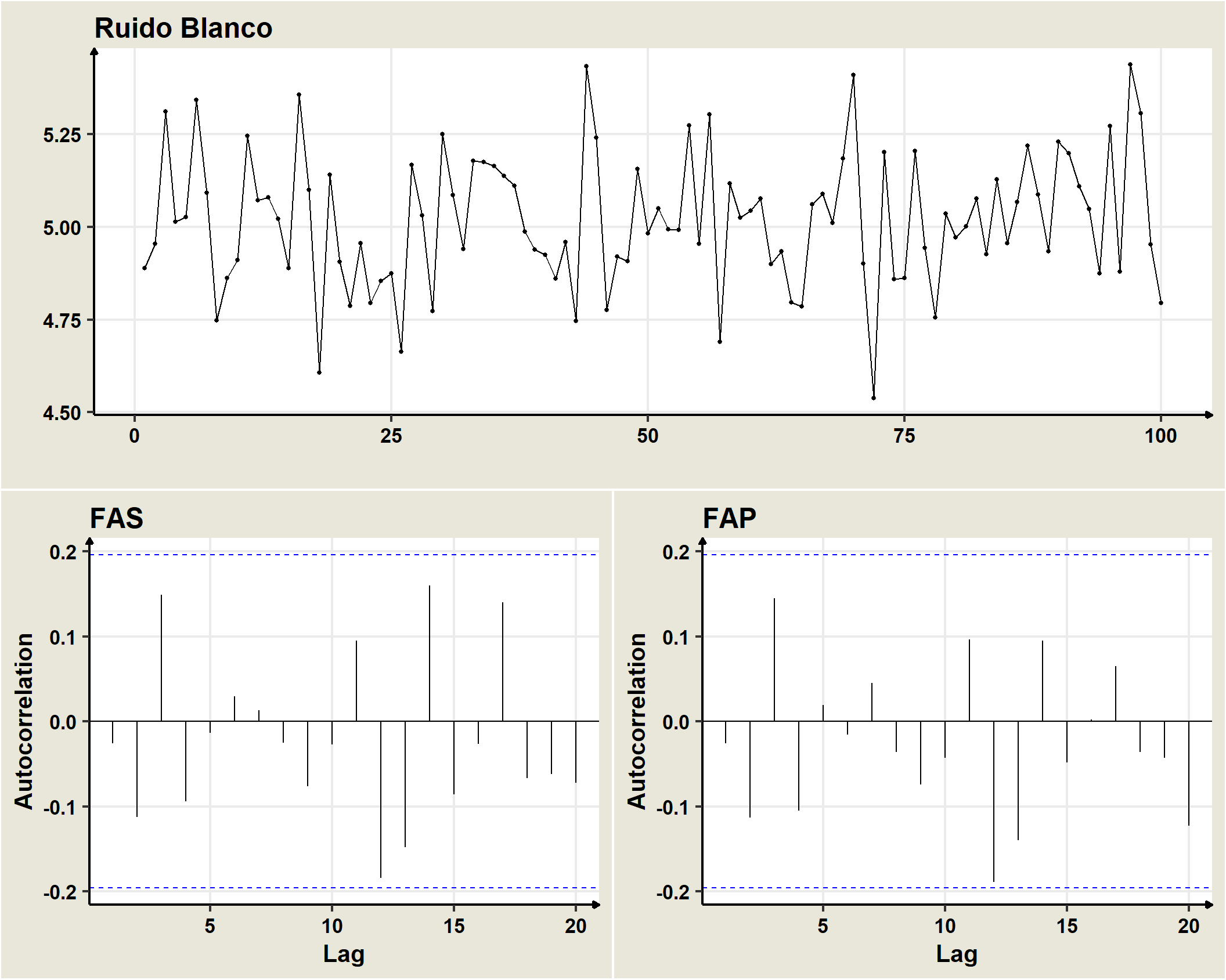
De manera general, un proceso de ruido blanco univariante es una secuencia $(\omega_t)$ de variables aleatorias idéntica e independientemente distribuidas con media $0$ y varianza $\sigma^2_\omega$, lo cual se representa como

$$\omega_t \sim IID(0,\sigma^2_\omega)$$

Cada $\omega_t$ sigue una distribución Normal, $(\omega_t)$ se denomina un proceso de ruido blanco Normal o Gaussiano.

Suponemos que los errores de los procesos que veremos a continuación son ruidos blancos gaussianos, formados por una sucesión de variables aleatorias con distribución Normal, esperanza cero, varianza constante e incorrelacionadas serialmente entre sí. Es decir, si $(\omega_t)$ es ruido blanco gaussiano, entonces $\omega_t \sim N(0,\sigma^2_\omega)$ y $cov(\omega_t,\omega_{t+k})=0.$