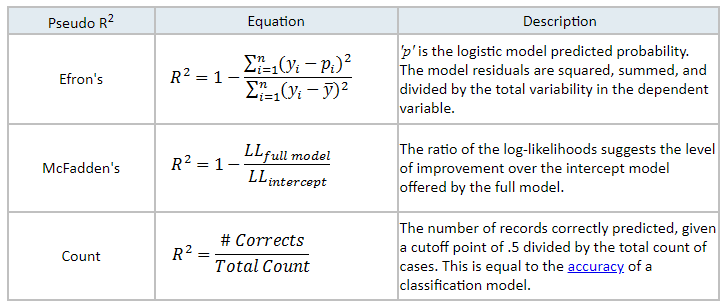
10.1 Pseudo \(R^2\)

A diferencia de los modelos de regresión lineal, en los modelos logísticos no se utiliza ni existe un equivalente a \(R^2\) que determine exactamente la varianza explicada por el modelo.

Se han desarrollado diferentes métodos conocidos como \(\operatorname{pseudo}-R^2\) que intentan aproximarse al concepto de coeficiente de determinación. Su rango oscila entre 0 y 1, pero de ninguna manera se pueden interpretar igual a \(R^2\).

Uno de los \(\operatorname{pseudo}-R^2\) más conocidos fue propuesto por McFadden’s:

\[ R^{2}_{\text{McFadden}} = 1- \frac{\log(L(M_1))}{\log(L(M_0))}, \]

donde \(L\) el valor de likelihood de cada modelo. La idea es que, \(\log(L)\), tiene un significado análogo a la suma de cuadrados de la regresión lineal. De ahí que se le denomine \(\operatorname{pseudo}-R^2\).

\(R^{2}_{\text{McFadden}}\)tiene valor \(0\) si el modelo ajustado no mejora al modelo nulo, y valor de \(1\) si se ajusta perfectamente a los datos.

• En el ejemplo de Venta de Vehículos:

\[\text{McFadden } R^2 = 0.142147,\]

Hay otros pseudo-\(R2\):