18.3 FAS y FAP

En el análisis de series temporales, el objetivo es identificar el proceso que subyace bajo los datos. Las herramientas para identificar a estos procesos son las funciones de autocorrelación simple (FAS) y parcial (FAP).

Dichas funciones se definen a partir de los coeficientes de autocorrelación. Ayudan a identificar cuáles son las observaciones que contribuyen para la formación del patrón de la serie temporal.

La función de autocorrelación simple (FAS) de una serie temporal mide la correlación entre observaciones separadas $1, 2,\ldots,n$ periodos.

la función de autocorrelación simple (fas) puede estimarse a partir de las autocovarianzas del proceso tal que:

$$\hat \rho_{k}=\frac{\hat \gamma_k}{\hat \gamma_0}$$

donde: $$\hat \gamma_0=\frac{\sum_{t=1}^{T}(Y_t-\bar Y)^2}{T}$$ $$\hat \gamma_k=\frac{\sum_{t=k+1}^{T}(Y_t-\bar Y)(Y_{t+k}-\bar Y)}{T-k}$$

La función de autocorrelación parcial (FAP) mide la correlación entre observaciones separadas $1, 2,\ldots,n$ periodos, excluyendo el efecto de las correlaciones intermedias.

Debe tenerse en cuenta que, parte de la correlación simple entre la variable $Y$ en un instante $t$ y un instante anterior $t-1$, puede deberse a la correlación existente de la variable con ella misma en instantes intermedios. Por ejemplo, puede que exista cierta correlación entre $Y_t$ e $Y_{t−2}$, debido a que ambas variables estén correlacionadas con $Y_{t−1}$.

En el caso de un AR(2):

$$\begin{array}{r l} Y_t = & \phi_1 Y_{t-1}+\phi_2 Y_{t-2}\\ = & \phi_1 (\phi_1 Y_{t-2}+\phi_2 Y_{t-3})+\phi_2 Y_{t-2}\\ = & \phi_1^2 Y_{t-2} +\phi_2 Y_{t-2} + \phi_1 \phi_2 Y_{t-3} \end{array}$$

• Existe un efecto directo de $Y_{t-2}$ sobre $Y_t$ a través de $\phi_2$
• Existe un efecto indirecto de $Y_{t-2}$ sobre $Y_t$ a través de $Y_{t-1},$ debido al hecho de que $Y_t$ e $Y_{t-1}$ están relacionados por $\phi_1.$
• Si $\phi_1=0$, no existiría relación entre $Y_t$ e $Y_{t-1},$ por lo que sólo existiría el efecto directo entre $Y_t$ e $Y_{t-2}.$
• Exite un efecto directo de $Y_{t-3}$ sobre $Y_t$ a través de $Y_{t-1}$ e $Y_{t-2}$

La correlación parcial entre dos variables de un conjunto es la correlación una vez eliminado el efecto de las correlaciones con las otras variables. En otras palabras, La FAP calcula la correlación directa eliminando posibles dependencias asociadas a retardos intermedios.

El correlograma es la representación gráfica de los coeficientes de autocorrelación en función de los distintos retardos de la serie temporal. Permiten representar las funciones FAS y FAP.

Un correlograma sólo tiene sentido dentro del ámbito de los procesos estacionarios porque asumen que la correlación entre dos valores de la serie solo depende de su distancia, no del instante de tiempo al que van referidos.

Un ejemplo:

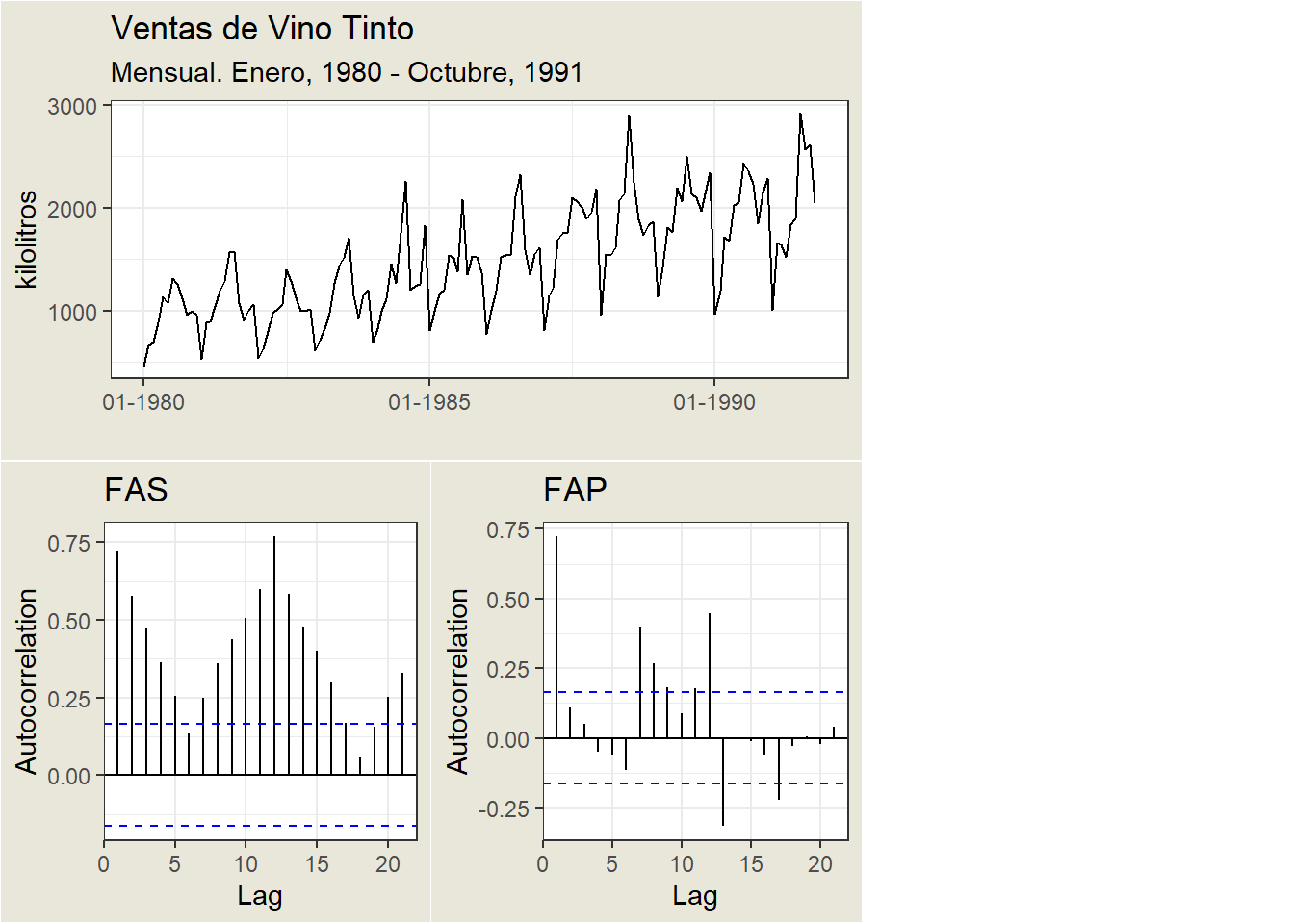
• El eje x del gráfico de FAS indica el retardo en el que se calcula la autocorrelación; el eje y indica el valor de la correlación (entre -1 y 1). Por ejemplo, un pico en el retardo 1 de un gráfico de FAS indica que existe una fuerte correlación entre el valor de cada serie y el valor anterior, un pico en el retardo 2 indica que existe una fuerte correlación entre el valor de cada serie y el valor que aparece dos instantes anteriores, etc.

• Una correlación positiva indica que los valores grandes actuales se corresponden con valores grandes en el retardo especificado; una correlación negativa indica que los valores grandes actuales se corresponden con valores pequeños en el retardo especificado.

• El valor absoluto de una correlación es una medida de la fuerza de la asociación, con valores absolutos mayores que indican relaciones más fuertes.